Взаимное или обратное очень полезно во всех видах алгебраических уравнений. Например, когда вы делите одну дробь на другую, вы умножаете первую дробь на обратную величину второй. Вам также необходимо использовать обратное при поиске уравнения линии.
Шаг
Метод 1 из 3: поиск обратной дроби или целого числа
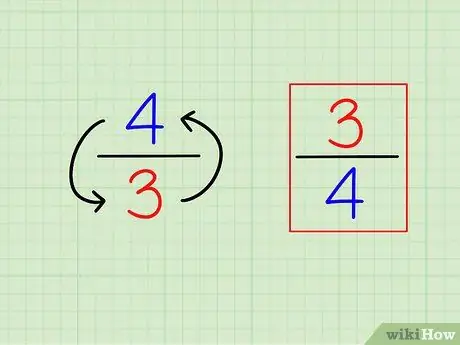
Шаг 1. Найдите обратную дробь, инвертируя ее
Определить «взаимно» или наоборот очень просто. Чтобы найти обратное к любому целому числу, просто вычислите «1 (это число)». Для дробей обратная величина - это другая дробь, то есть числа являются «инвертированными» (инверсными).
- Например, противоположность 3/4 является 4/3.
- Любое число, умноженное на обратное, возвращает 1.
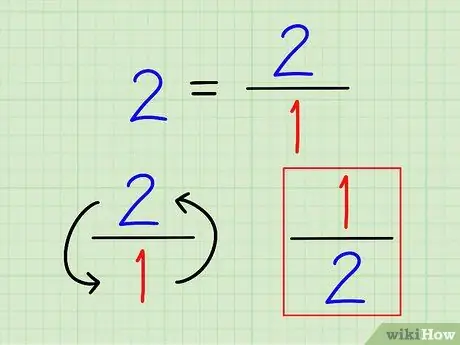
Шаг 2. Запишите обратную величину целого числа в виде дроби
Опять же, обратное значение числа всегда равно 1 (это число). Целые числа записывайте как дроби. Нет смысла вычислять это число до десятичной дроби.
Например, 2 равно 1 2 = 1/2.
Метод 2 из 3: поиск обратного значения смешанной дроби
Шаг 1. Определите смешанные числа
Смешанные дроби состоят из целых чисел и дробей, например 24/5. Как описано ниже, есть два шага к нахождению обратной величины смешанного числа.
Шаг 2. Преобразуйте смешанные числа в неправильные дроби
Помните, что 1 всегда можно записать как (число) / (одно и то же число), а дроби с одинаковым знаменателем (нижнее число) можно складывать вместе. Вот пример использования 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
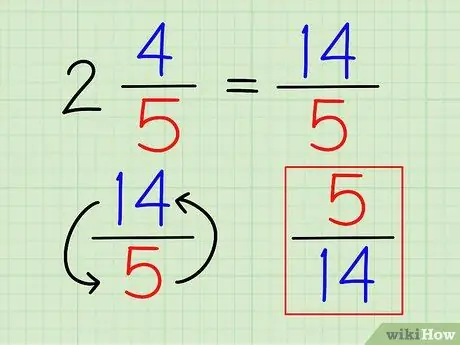
Шаг 3. Переверните дробь
После того, как число полностью записано как дробь, вы можете найти его обратную величину, как и любую другую дробь, перевернув дробь.
В приведенном выше примере величина, обратная 14/5 является 5/14.
Метод 3 из 3: поиск противоположности десятичной дроби
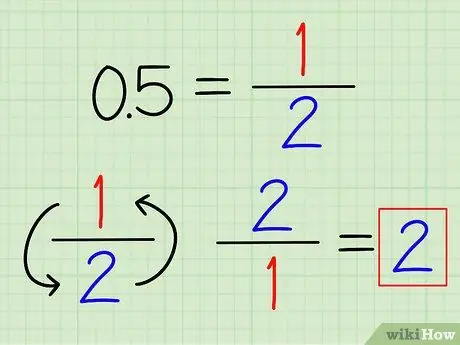
Шаг 1. Преобразуйте десятичные дроби в дроби, если это возможно
Вы можете узнать некоторые часто используемые десятичные числа, которые можно легко преобразовать в дроби. Например, 0,5 = 1/2 и 0,25 = 1/4. После преобразования десятичной дроби в дробь просто переверните дробь, чтобы найти обратную дробь.
Например, величина, обратная 0,5, равна 2/1 = 2.
Шаг 2. Напишите задачу о делении
Если вы не можете преобразовать его в дробь, вычислите обратную величину числа в виде задачи деления: 1 (десятичный). Вы можете использовать калькулятор, чтобы решить эту проблему, или перейти к следующему шагу, чтобы решить ее вручную.
Например, вы можете найти обратную величину 0,4, вычислив 1 0,4
Шаг 3. Измените задачу деления на целые числа
Первым шагом к разделению десятичных дробей является перемещение десятичной точки, пока все числа не станут целыми числами. Если вы переместите десятичную точку обоих чисел на одинаковое количество шагов, вы получите правильный ответ.
Например, вы можете использовать 1 0, 4 и переписать его как 10 4. В этом случае вы перемещаете все десятичные разряды на один шаг вправо, точно так же, как вы умножаете каждое число на десять
Шаг 4. Решите задачу с помощью длинного деления
Используйте метод длинного деления, чтобы вычислить обратную величину. Если вы посчитаете 10 4, вы получите ответ 2, 5 что является обратной величиной 0, 4.
подсказки
- Отрицательная обратная величина числа такая же, как и обычная обратная величина, в том смысле, что она умножается на отрицательную единицу. Например, отрицательная величина, обратная 3/4 является -4/3.
- Обратное или обратное часто называют «обратным умножением».
- Число 1 противоположно самому себе, потому что 1 1 = 1.
- Число 0 не имеет обратного значения, потому что 0 не определено.
