- Автор Jason Gerald [email protected].
- Public 2023-12-16 11:35.
- Последнее изменение 2025-01-23 12:44.
В десятичной (десятичной) системе счисления есть десять возможных значений (0, 1, 2, 3, 4, 5, 6, 7, 8 или 9) для каждой числовой позиции. В отличие от этого, двоичная система счисления (с основанием два) имеет только два возможных значения, представленных 0 и 1 для каждой числовой позиции. Поскольку двоичная система счисления является внутренним языком электронных компьютеров, серьезные программисты знают, как преобразовать десятичную систему счисления в двоичную. Следуйте этим простым шагам, а также как освоить это преобразование.
Шаг
Метод 1 из 2: деление на два с остатком

Шаг 1. Определите проблему
В этом примере давайте преобразуем десятичное число 15610 быть двоичным числом. Запишите десятичное число как число, которое нужно разделить, в виде перевернутого символа деления. Запишите основание целевой системы счисления (в этом примере «2» для двоичной) как делитель вне кривой символа деления.
- Этот метод намного легче понять, когда он нарисован на бумаге, и намного проще для начинающих, потому что он делится только на два.
- Чтобы избежать путаницы до и после преобразования, запишите базовое число вычисляемой вами системы счисления в виде нижнего индекса (строчные буквы под обычными буквами в качестве отличительного знака) для каждого числа. В этом примере десятичное число будет иметь нижний индекс 10, а двоичное число будет иметь нижний индекс 2.

Шаг 2. Делаем деление
Напишите целочисленный ответ (частное) под символом длинного деления и запишите остаток (0 или 1) справа от разделенного числа.
Поскольку мы делим на два, когда делимое число является четным, остаток равен 0, а когда делимое число является нечетным числом, остаток равен 1

Шаг 3. Продолжайте деление до нуля
Продолжайте спуск, деля каждое новое частное на два и записывая остаток справа от каждого деленного числа. Остановитесь, когда частное будет равно нулю.

Шаг 4. Запишите новое двоичное число
Начиная с наименьшего оставшегося числа, прочтите порядок остатка в возрастающем порядке вверх. В этом примере вы должны получить результат 10011100. Это двоичный эквивалент десятичного числа 156. Или, если записано с его числовым нижним индексом: 15610 = 100111002.
Этот метод можно изменить для преобразования десятичного основания в любое числовое. Делитель равен 2, потому что основание целевой системы счисления - 2 (двоичное). Если основание системы счисления назначения является другим основанием, замените число с основанием 2 в этом методе на соответствующее число с основанием. Например, если база назначения - это база 9, замените число с основанием 2 на 9. Окончательный результат будет непосредственно в форме базового числа назначения
Метод 2 из 2: вычисление степени двойки и вычитание

Шаг 1. Начнем с создания таблицы
Запишите степени двух основных чисел в «базе таблицы 2» справа налево. Начать с 20запишите его как «1». Повышайте ранг на 1 за каждый ранг. Заполняйте таблицу, пока не получите число, наиболее близкое к числу в десятичной системе счисления, которую вы вычисляете. В этом примере давайте преобразуем десятичное число 15610 быть двоичным числом.

Шаг 2. Найдите число с наибольшей степенью основания 2
Из таблицы выберите наибольшее число, которое равно или меньше числа, которое нужно преобразовать. Число 128 - это число с наибольшей степенью основания числа 2, которое также меньше 156, поэтому напишите число «1» под этим полем в таблице, где наибольшее число из таблицы находится слева (см. Таблицу на изображении выше). Затем вычтите 128 из начального числа, и вы получите: 156 - 128 = 28.
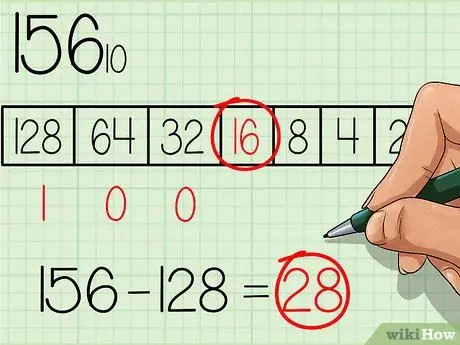
Шаг 3. Перейти к следующему меньшему значению в таблице
Используя новое число (28), продолжайте просматривать таблицу слева направо, проверяя, равны ли числа новому числу или меньше него. Число 64 не меньше 28, поэтому напишите цифру «0» под числовым полем 64. Продолжайте, пока не найдете число, равное или меньшее 28.
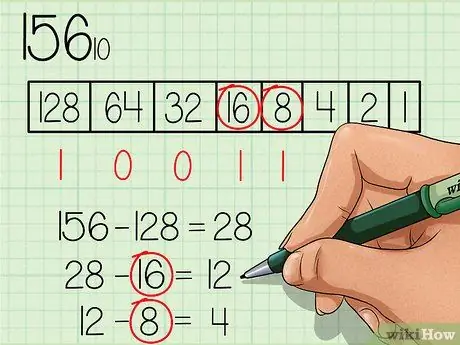
Шаг 4. Вычтите каждое число, которое равно или меньше нового числа, и отметьте цифру «1» под окном соответствующего числа
Число 16 меньше 28, поэтому напишите число «1» под числовым полем 16 и вычтите 16 из 28, чтобы получить новое число 12. Число 8 меньше 12, поэтому напишите число «1» под числовое поле 8 и вычтите 8 из 12, чтобы получить новое число 4.

Шаг 5. Продолжайте, пока не дойдете до конца стола
Не забудьте отметить «1» под каждым полем для чисел, которые равны или меньше нового числа, и «0» под каждым полем для чисел, которые все еще больше нового числа.
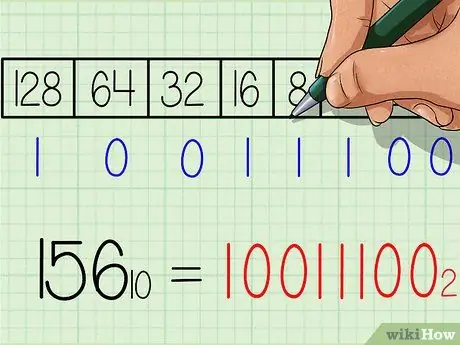
Шаг 6. Запишите ответ на двоичное число
Число слева направо будет точно таким же, как и ряд чисел «1» и «0» внизу таблицы. Вы должны получить результат 10011100. Это двоичный эквивалент десятичного числа 156. Или при записи с нижним индексом: 15610 = 100111002.
Повторение этого метода поможет вам запомнить силы двух оснований, поэтому шаг 1 можно пропустить
подсказки
- Программа калькулятора, встроенная в операционную систему, может выполнить это преобразование за вас, но, как программисту, лучше всего начать с хорошего понимания того, как работают преобразования. Параметры преобразования в программе калькулятора можно сделать видимыми, открыв меню «Вид» и выбрав «Программист» (для Windows 7 и 8).
- Преобразование в обратном направлении, то есть из двоичной системы счисления в десятичную, обычно легче сначала выучить.
- Часто практикуйте преобразование десятичных чисел в двоичные, чтобы стать более опытным.






