Разве вы не знаете, как рисовать линейные уравнения без использования калькулятора? К счастью, построить графики линейных уравнений довольно просто, если вы знаете, как это сделать. Все, что вам нужно сделать, это понять кое-что о своем уравнении, и вы сможете это сделать. Давайте начнем.
Шаг
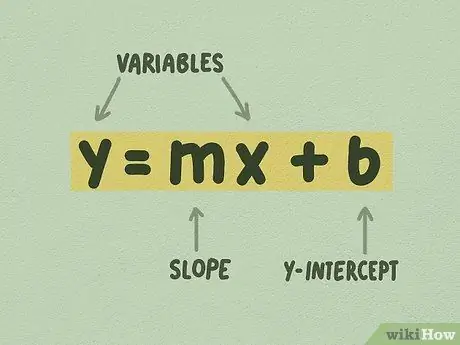
Шаг 1. Убедитесь, что линейное уравнение имеет вид y = mx + b
Эта форма называется формой пересечения по оси Y и, вероятно, является самой простой формой для построения графиков линейных уравнений. Значение в уравнении не обязательно должно быть целым числом. Часто вы увидите уравнение, которое выглядит так: y = 1 / 4x + 5, где 1/4 - это m, а 5 - это b.
- м называют «уклоном», а иногда и «уклоном». Наклон определяется как увеличение по краю или изменение y, деленное на изменение x.
- b определяется как «точка пересечения с y». Y-пересечение - это точка, в которой линия пересекает ось Y.
- x и y - переменные. Вы можете найти конкретное значение x, например, если у вас есть точка y и известны значения m и b. Однако у x никогда не бывает только одного значения: его значение изменяется по мере того, как линия идет вверх или вниз.
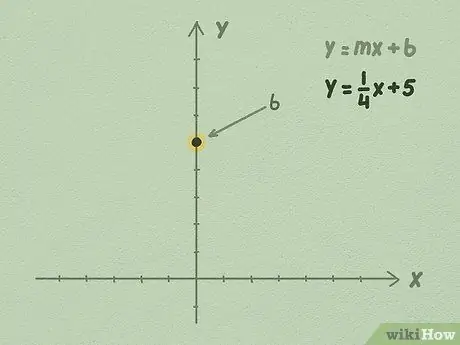
Шаг 2. Нарисуйте число b на оси Y
Ваше значение b всегда будет рациональным числом. Каким бы ни было число b, найдите его значение на оси Y и поместите число в точку на вертикальной оси.
Например, давайте использовать уравнение y = 1 / 4x + 5. Поскольку последнее число - b, мы знаем, что b равно 5. Переместитесь на 5 точек вверх по оси Y и отметьте точки. Здесь ваша прямая линия пересечет ось Y
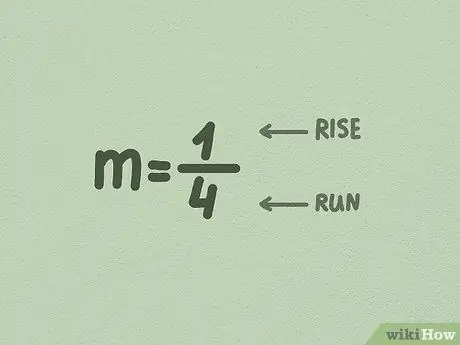
Шаг 3. Преобразовать m в дробь
Часто число перед x уже является дробной частью, поэтому вам не нужно его менять. Но если нет, просто измените его, поместив значение m под цифрой 1.
- Первое число (числитель) - это приращение по возрастанию, разделенное на сторону. Это число указывает, насколько далеко линия идет вверх или по вертикали.
- Второе число (знаменатель) - это сторона по возрастанию, разделенная на сторону. Это число указывает, насколько далеко линия перемещается вбок или по горизонтали.
- Например:
- Наклон 4/1 сдвигает на 4 пункта вверх на каждый 1 пункт в сторону.
- Наклон -2/1 сдвигает на 2 пункта вниз за каждую 1 точку в сторону.
- Наклон 1/5 сдвигает на 1 пункт вверх на каждые 5 пунктов в сторону.
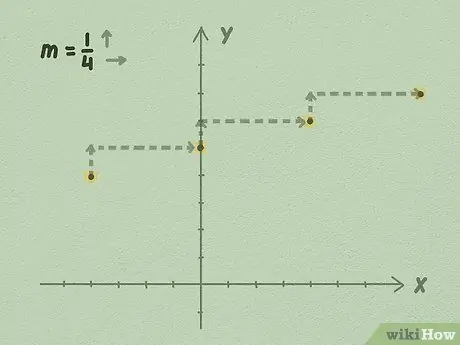
Шаг 4. Начните вытягивать линию от точки b, используя уклон, или вверх, разделенную сторонами
Начните со своего значения b: мы знаем, что уравнение выходит за рамки этой точки. Продлите линию, взяв свой наклон и используя его значение, чтобы получить точки в уравнении.
- Например, используя иллюстрацию выше, вы можете увидеть, что на каждую 1 точку вверх линия перемещается на 4 точки вправо. Это происходит потому, что наклон линии равен 1/4. Вы продлеваете линию до бесконечности в обе стороны, продолжая использовать разделенное по сторонам, чтобы построить линию.
- Наклон положительный при движении вверх и отрицательный при движении вниз. Например, наклон -1/4 будет снижаться на 1 пункт на каждые 4 пункта в сторону.
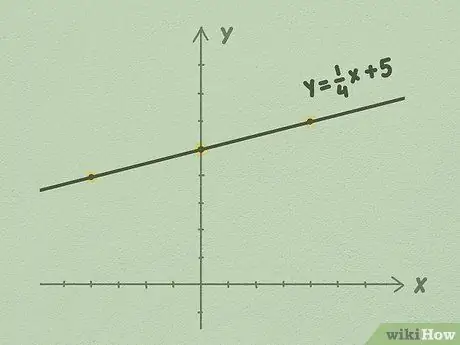
Шаг 5. Продолжайте вытягивать линию с помощью линейки и обязательно используйте наклон m в качестве ориентира
Вытяните линию до бесконечности, и вы закончите рисовать линейное уравнение. Довольно просто, правда?
