- Автор Jason Gerald [email protected].
- Public 2024-01-15 08:22.
- Последнее изменение 2025-06-01 06:07.
Вы можете подумать, что целые числа - это просто обычные числа, например 3, -12, 17, 0, 7000 или -582. Целые числа также называют целыми числами, потому что они не делятся на части, такие как дроби и десятичные дроби. Прочтите эту статью, чтобы узнать все, что вам нужно, о сложении и вычитании целых чисел, или прочтите непосредственно нужный вам раздел.
Шаг
Метод 1 из 5: сложение и вычитание положительных целых чисел с помощью числовой строки

Шаг 1. Узнайте о числовой прямой
Числовые линии превращают основную математику в нечто осязаемое и физическое, что вы можете видеть. Имея всего несколько знаков и здравый смысл, мы можем использовать его как калькулятор для сложения и вычитания чисел.

Шаг 2. Проведите базовую числовую линию
Представьте или проведите ровную прямую линию. Сделайте точку посередине линии. Напишите 0 или ноль рядом с этим периодом.
В вашей книге по математике это может быть отправная точка, потому что это отправная точка для всех чисел

Шаг 3. Нарисуйте две точки, по одной справа и слева от нуля
Напишите - 1 рядом с точкой слева и
Шаг 1. рядом с точкой справа. Это целое число, наиболее близкое к нулю.
- Не беспокойтесь о том, чтобы расстояния между точками были одинаковыми - если вы знаете, что означает каждая точка, можно использовать числовую линию.
- Левая часть - это начало предложения.

Шаг 4. Заполните числовую строку, добавив дополнительные числа
Сделайте больше точек слева, чем -1, и справа, чем 1. Слева, от -1, отметьте ваши точки с помощью - 2, - 3, а также - 4. Справа от 1 отметьте точку знаком
Шаг 2
Шаг 3., да
Шаг 4.. Вы можете продолжить, если у вас есть место на бумаге.
Пример на рисунке показывает числовую линию от -6 до 6

Шаг 5. Узнайте о положительных и отрицательных целых числах
Положительные целые числа, также называемые натуральное число, является целым числом больше нуля. 1, 2, 3, 25, 99 и 2007 - положительные целые числа. Отрицательные целые числа - это целые числа, которые меньше нуля (например, -2, -4 и -88).
Целые числа - это еще один способ вызова целых чисел. Такие дроби, как 1/2 (половина), являются лишь частью числа, поэтому они не являются целыми числами. То же, что и десятичное, например 0,25 (ноль целых две и пять десятых долей); десятичное число не является целым числом

Шаг 6. Начните решать 1 + 2, поместив палец на точку 1
Решим простые задачи сложения 1+2 используя только что созданную числовую линию. Первое число
Шаг 1., так что начните указывать пальцем на номер.
-
Это слишком простой вопрос?
Если вы когда-либо добавляли, вы, вероятно, знаете ответ на вопрос 1 + 2. Хорошо: если вы знаете результат, вам будет легче понять, как работает числовая прямая. Затем вы можете использовать числовую прямую для решения более сложных задач на сложение или для подготовки к более сложной математике, такой как алгебра.

Шаг 7. Сложите 1 + 2, переместив палец на 2 точки вправо
Проведите пальцем вправо, считая количество пройденных точек (другое число). Если вы прошли 2 новых пункта, остановитесь. Число, на которое указывает ваш палец, и есть ответ,
Шаг 3
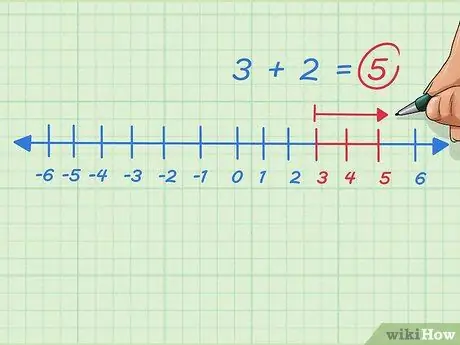
Шаг 8. Добавьте любые положительные целые числа, перемещаясь вправо на числовой строке
Предположим, мы хотим решить 3 + 2. Начните с 3, двигайтесь вправо или добавьте 2 точки. Останавливаемся на 5. Задача написана 3 + 2 = 5.

Шаг 9. Вычтите положительные целые числа, сдвинув числовую строку влево
Например, мы хотим решить 6-4, мы начинаем с 6, перемещаемся влево на 4 пункта и останавливаемся на 2. В этой задаче написано 6-4 = 2.
Метод 2 из 5: сложение и вычитание отрицательных чисел с помощью числовой линии

Шаг 1. Узнайте о числовых линиях
Если вы не знаете, как создать числовую линию, вернитесь к разделу «Сложение и вычитание положительных чисел с помощью числовых линий», чтобы узнать, как ее создать.
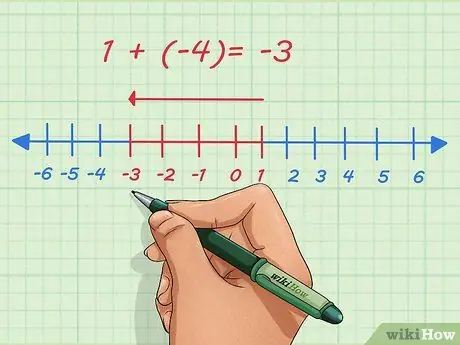
Шаг 2. Узнайте об отрицательных числах
Положительные числа обозначаются направлением вправо на числовой прямой. Отрицательные числа указываются слева в числовой строке. Добавление отрицательных чисел означает перемещение точки влево на числовой прямой.
-
Например, добавим 1 и -4. Обычно этот вопрос пишется так:
1 + (-4)
. На числовой прямой мы начинаем с 1, перемещаемся на 4 точки влево и останавливаемся на -3.
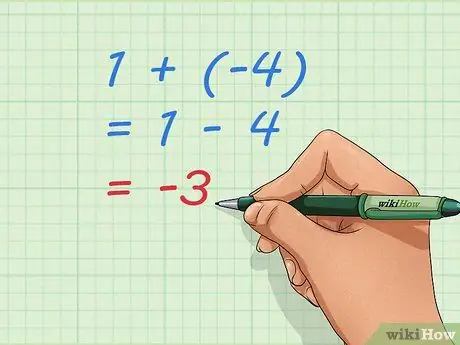
Шаг 3. Используйте основные уравнения, чтобы понять сложение отрицательных чисел
Обратите внимание, что -3, наш ответ, - это число, которое мы получим, если сделаем от 1 до 4. Сложение 1 + (-4) и вычитание 4 из 1 - та же проблема. Мы можем записать это в виде уравнения, математического предложения, которое показывает равенство: 1 + (-4) = 1-4 = -3
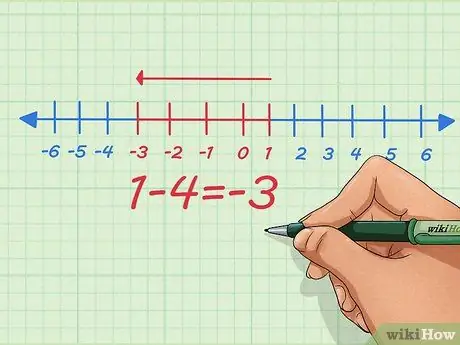
Шаг 4. Вместо того, чтобы складывать отрицательные числа, превратите это в задачу вычитания, используя положительные числа
Как видно из приведенного выше простого уравнения, мы можем сделать и то, и другое - превратить сложение отрицательных чисел в вычитание положительных и наоборот. Возможно, вас учили превращать негатив в негатив, не зная почему - вот почему.
-
Например, -4. Когда мы складываем -4 и 1, мы вычитаем 1 на 4. Это можно записать математически, написав
1 + (-4) = 1 - 4
. Мы можем написать это в числовой строке, начиная с начальной точки с 1, а затем добавив 4 точки слева (другими словами, добавив -4). Поскольку это уравнение, одно равно другому, поэтому верно и обратное.
1 - 4 = 1 + (-4)
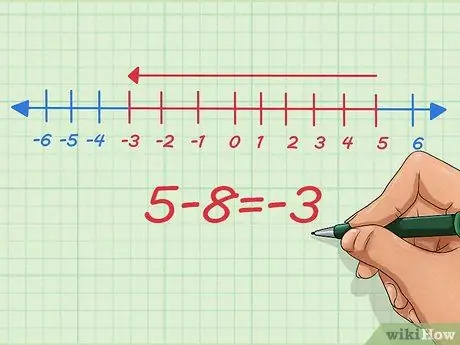
Шаг 5. Научитесь вычитать отрицательные числа на числовой прямой
В числовой строке вычитание отрицательных чисел аналогично уменьшению длины. Начнем с 5-8.
На числовой строке мы начинаем с нашей начальной точки с 5, вычитаем 8 и останавливаемся на -3
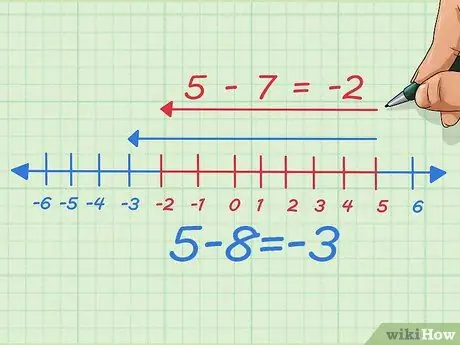
Шаг 6. Вычтите вычитаемую сумму и посмотрите, что произойдет
Предположим, мы вычитаем единицу, число, которое мы вычитаем, или, другими словами, вычитаем 7 вместо 8. Теперь мы вычитаем одну точку слева на числовой прямой. В письменной форме мы начали с 5-8 = -3 Теперь мы просто перемещаем 7 влево, так что получается 5-7 = -2.
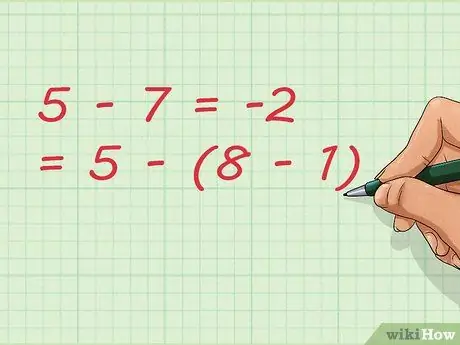
Шаг 7. Обратите внимание, что вычитание может привести к сложению
В нашем примере мы вычитаем число 1. При написании уравнения мы можем записать его короче, например: 5-7 = -2 = 5 - (8-1)

Шаг 8. Преобразуйте отрицательные знаки в положительные при добавлении отрицательных чисел
Используя этап преобразования всех вычитаний в сложения, мы можем записать более короткие, например: 5 - (8-1) = 5-7 = 5-8 + 1.
-
Мы уже знаем, что 5-8 = -3, поэтому возьмите 5-8 из уравнения и введите -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Мы уже знаем, что 5 - (8-1) равно - вычитает один балл из 5-8. Наше уравнение может показать, что 5-8 равно -3, а вычитание одного балла дает -2. Уравнение можно записать так:
-3 - (-1) = -3 + 1
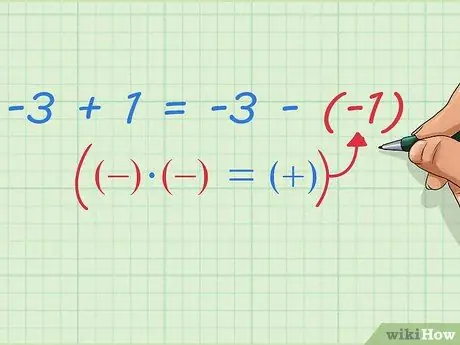
Шаг 9. Запишите вычитание отрицательных чисел как сложение
Обратите внимание на то, что происходит после этого - мы уже доказали, что: -3 + 1 = -3 - (-1) Мы можем написать это с помощью более простых и общих математических правил написания: первое число плюс второе число = первое число минус (второе отрицательное число) Или более простой способ, который вы, вероятно, слышали на уроках математики: Измените два отрицательных знака на положительный.
Метод 3 из 5: сложение больших положительных целых чисел

Шаг 1. Напишите задачу сложения 2 503 + 7 461, поставив одно число над другим
Запишите числа в большом столбце так, чтобы 2 было больше 7, 5 больше 4 и т. Д. Таким образом, мы узнаем, как складывать целые числа, которые слишком велики, чтобы представить или использовать числовую строку.
Напишите знак + слева от числа ниже и строки под ним, как вы, возможно, научитесь решать более мелкие задачи сложения
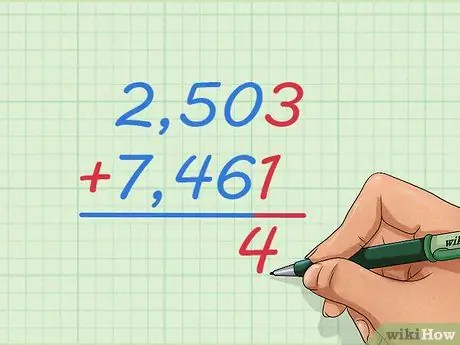
Шаг 2. Начните с сложения двух чисел справа
Было бы немного странно начинать справа, потому что мы читаем числа слева. Мы должны добавить справа, чтобы получить правильный ответ, который вы увидите позже.
-
Под двумя крайними правыми числами
Шаг 3. да
Шаг 1.запишите сумму двух
Шаг 4..

Шаг 3. Таким же образом сложите каждое число в столбце
Двигайтесь влево, складывайте 0+6, 5+4, а также 2+7. Напишите ответ под каждой парой чисел.
Ваш ответ должен быть таким: 9.964. Если вы ошиблись, проверьте свою работу.

Шаг 4. Теперь сложите 857 + 135
Вы заметите что-то другое, как только сложите первую пару чисел справа. 7+5 равно 12, двузначное число, но вы можете написать только одну цифру в этом столбце. Продолжайте читать, чтобы узнать, что вам следует делать и почему всегда следует начинать справа, а не слева.

Шаг 5. Сложите 7 + 5 и узнайте, где написать ответ
7 + 5 = 12, но нельзя поставить 1 и 2 под чертой. Но запиши последнюю цифру, Шаг 2., под чертой запишите первую цифру
Шаг 1., над столбцом слева, 5 + 3.
-
Если вам интересно, как это работает, подумайте, что означает разделение 1 и 2. На самом деле вы делите 12 на
Шаг 10. да
Шаг 2.. Вы можете написать 10 над числом, если хотите, и вы увидите 1 в столбцах 5 и 3, как и раньше.

Шаг 6. Сложите 1 + 5 + 3, чтобы получить следующую цифру ответа
Теперь вам нужно сложить три цифры, потому что вы добавили 1 в этот столбец. Ответ
Шаг 9., поэтому ваш ответ будет 92.
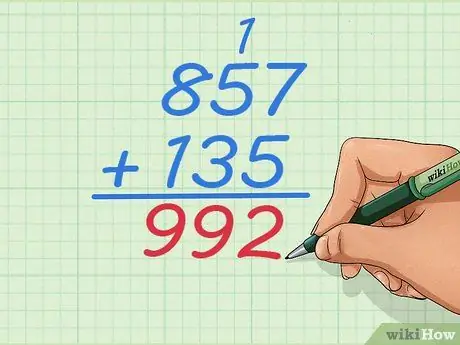
Шаг 7. Завершите задачу как обычно
Продолжайте работать с цифрами слева, пока не сложите все числа, в этом случае останется только один столбец. Ваш окончательный ответ должен быть 992.
- Вы можете задать более сложные вопросы, например 974 + 568. Помните, что всякий раз, когда вы получаете двузначное число, указывайте только последнюю цифру в качестве ответа и помещайте другую цифру над столбцом слева, которую вы будете складывать дальше. Если ответ в последнем столбце (крайний слева) состоит из двух цифр, запишите его как свой ответ.
- См. Раздел «Советы», чтобы найти ответы на вопросы 974 + 568 после того, как вы попытались их решить.
Метод 4 из 5: вычитание больших положительных целых чисел

Шаг 1. Напишите задачу на вычитание 4,713-502, указав первое число над вторым числом
Напишите так, чтобы 3 было прямо над 2, 1 было над 0, 7 было над 5, а 4 было над пробелом.
Вы можете написать 0 под 4, если это поможет вам запомнить, какое число выше какого числа. Вы всегда можете добавить 0 перед числом, не меняя его. Обязательно добавляйте его перед числом, а не после него

Шаг 2. Вычтите каждое число ниже из числа прямо над ним
Всегда начинайте справа. Решите 3-2, 1-0, 7-5 и 4-0, запишите ответ на каждый вопрос прямо под двумя вычтенными числами.
В результате 4.211.

Шаг 3. Теперь таким же образом напишите вопросы 924-518
В этих числах одинаковое количество цифр, поэтому вы можете легко их записать. Эта задача научит вас кое-чему о вычитании целых чисел, если вы этого еще не знаете.

Шаг 4. Узнайте, как решить первую задачу, которая находится справа
4-8. Эта проблема сложна, потому что 4 меньше 8, но не используйте отрицательные числа, а выполните следующие действия:
- В верхнем ряду скрестите 2 и напишите 1. 2 должно быть слева от 4.
- Перекрестите 4 и напишите 14. Сделайте это в узком месте, чтобы было ясно, что 14 больше 8. Вы также можете написать 1 перед 4, чтобы получилось 14, если места достаточно.
- Вы только что заимствовали 1 из разряда десятков или второго столбца справа и преобразовали его в 10 в разряде единиц или крайнем правом столбце. Если число 10 равно десятикратному числу 1, значит, оно то же самое.

Шаг 5. Теперь решите задачи 14-8 и запишите ответ в крайнем правом столбце
В правой строке ответа должно было быть написано 6.

Шаг 6. Заполните следующий столбец слева, используя записанный вами новый номер
Вычитание должно быть 1 - 1, что равно 0.
Теперь ваш ответ должен быть 06.

Шаг 7. Решите задачу, выполнив последнее вычитание в крайнем левом столбце
9 - 5 = 4, поэтому ваш окончательный ответ 406.

Шаг 8. Теперь решаем задачу вычитания больших чисел из маленьких
Предположим, вас просят заполнить 415 990 - 968 772. Напишите второе число под первым числом, и вы поймете, что число ниже больше! По первой цифре слева сразу видно: 9 больше 4, поэтому числа, начинающиеся с 9, больше.
Перед сравнением убедитесь, что вы правильно записали столбец. 912 нет больше 5000, вы можете сказать, правильно ли вы записываете столбец, потому что нет чисел ниже 5. Вы можете добавить нулевую справку, например, написать 912 с 0912, чтобы столбец равнялся 5000.

Шаг 9. Напишите меньшее число под большим числом и поставьте знак - перед ответом
Всякий раз, когда вы вычитаете число из меньшего числа, результатом будет отрицательное число. Этот знак лучше записать перед вычитанием, чтобы не забыть его записать.

Шаг 10. Чтобы ответить, вычтите маленькое число из большого числа и не забудьте написать знак -
Ваш ответ будет отрицательным, что обозначено знаком -. Не надо пытается вычесть большое число из маленького, а затем делает результат отрицательным; ваш ответ будет неправильным.
Новая задача, которую необходимо решить: 968 772 - 415 990 = -? См. Раздел «Советы», чтобы получить ответ после попытки решить эту проблему
Метод 5 из 5: сложение и вычитание отрицательных целых чисел
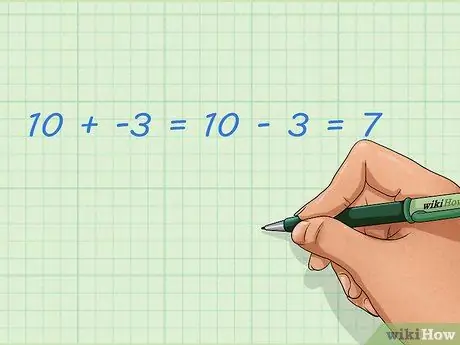
Шаг 1. Узнайте, как складывать отрицательные и положительные числа
Добавление отрицательных целых чисел аналогично вычитанию положительных целых чисел. Это проще сделать с числовой линией, описанной в другом разделе, но вы тоже можете придумать это на словах. Отрицательные числа - это не обычные числа; это число меньше нуля и может представлять взятую сумму. Если вы добавите этот дубль к обычному числу, результат станет меньше.
- Пример: 10 + -3 = 10-3 = 7
- Пример: -12 + 18 = 18 + -12 = 18 - 12 = 6. Помните, что вы всегда можете изменить порядок чисел при добавлении, но не при вычитании.
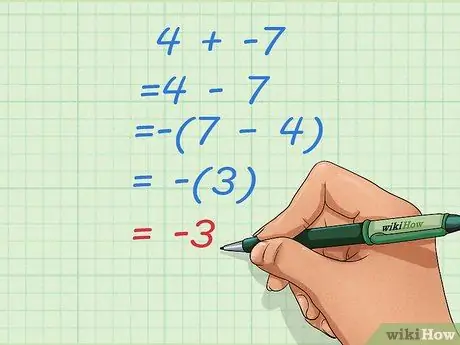
Шаг 2. Узнайте, что вам нужно сделать, если вы превратите это в задачу на вычитание с меньшим начальным числом
Иногда изменение сложения в задачах на вычитание, подобных приведенной выше, может привести к получению нечетных ответов, например 4-7. Когда это произойдет, поменяйте порядок чисел на обратный и сделайте результат отрицательным.
- Допустим, ваша начальная проблема - 4 + -7.
- Превратите это в задачу на вычитание: 4-7
- Поменяйте порядок и сделайте результат отрицательным: - (7 - 4) = - (3) = -3.
- Если вы не знакомы с использованием скобок в уравнениях, подумайте вот о чем: 4-7 превращается в 7-4 с добавлением отрицательного знака. 7-4 = 3, но мы должны изменить его на -3, чтобы ответ на вопросы 4-7 был правильным.
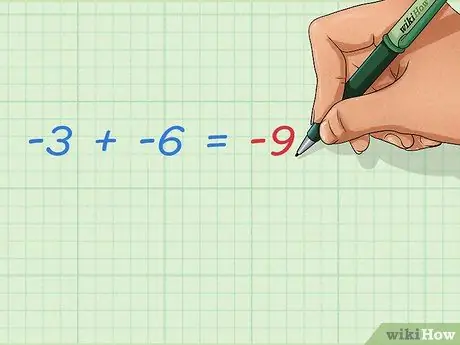
Шаг 3. Узнайте, как сложить два отрицательных целых числа
Два сложенных отрицательных числа всегда увеличивают отрицательный результат. Поскольку положительные числа не добавляются, результат будет дальше от 0. Ответ прост:
- -3 + -6 = -9
- -15 + -5 = -20
- Вы видите закономерность? Все, что вам нужно сделать, это сложить числа, как если бы они были положительными числами, и добавить отрицательный знак. -4 + -3 = - (4 + 3) = -7
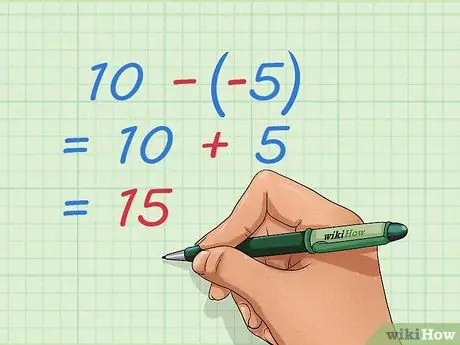
Шаг 4. Научитесь вычитать отрицательные целые числа
Как и в случае с проблемой сложения, вы можете переписать задачу так, чтобы у вас были только положительные числа. Если вы вычтите отрицательные числа, вы уберете некоторые из вещей, которые уже были взяты, что аналогично сложению положительных чисел.
- Считайте отрицательные числа украденными деньгами. Если вы вычитаете или забираете украденные деньги, чтобы их можно было вернуть, это все равно что отдать деньги кому-то, не так ли?
- Пример: 10 - -5 = 10 + 5 = 15
- Пример: -1 - -2 = -1 + 2. Вы уже узнали, как решить эту задачу на первом шаге, помните? Перечитайте, как складывать отрицательные и положительные числа, если вы забыли.
- Вот полное решение последнего примера: -1 - -2 = -1 + 2 = 2 + -1 = 2-1 = 1.
подсказки
- Вы могли написать длинные числа, например 2,521,301, используя запятые (,) вместо (.), В зависимости от того, где вы живете. Используйте то, что просит вас учитель, чтобы вас не путали с другими системами письма.
- Нарисуйте числовые линии в разных масштабах, чтобы обозначить разные числа. Не существует правила, согласно которому каждое расстояние на числовой прямой равно 1. Представьте числовую прямую, в которой 10 вместо 1. Помимо того, что теперь каждая точка равна 10, сложение и вычитание остаются прежними. Попробуйте, если не верите.
- Если вы попробуете ответить на специальные сложные вопросы в разделе «Длинные числа», вот ответ: 974 + 568 = 1.542. Ответ от 415 990 до 968 772: - 552.782.






