Дроби легко умножать на смешанные или целые числа. Начните с преобразования смешанных дробей или целых чисел в неправильные дроби (дроби с большим числителем, чем знаменатель). Умножьте числитель двух дробей. После этого умножьте два знаменателя и упростите произведение.
Шаг
Метод 1 из 2: умножение двух смешанных дробей
Шаг 1. Преобразуйте смешанные дроби в неправильные дроби
Чтобы преобразовать смешанное число, умножьте знаменатель на существующее целое число. После этого добавьте к произведению числитель. Поместите окончательный результат над линией и не меняйте знаменатель. Повторите этот шаг для других смешанных фракций.
Например, если у вас есть задача умножения 1 1/2 x 4 4/7, преобразуйте обе дроби в неправильные дроби. Дробь 1 1/2 может быть изменена на 3/2, а дробь 4 4/7 заменена на 32/7. Теперь ваша задача умножения становится 3/2 x 32/7
Шаг 2. Умножьте числитель обеих дробей
Если у вас есть две неправильные дроби и больше нет целых чисел в задаче, умножьте два числителя. Напишите результат и поместите его над линией.
- Числитель всегда стоит вверху дроби.
- Например, для задачи 3/2 x 32/7 умножьте 3 на 32, чтобы получить 96.
Шаг 3. Умножьте знаменатели обеих дробей
Теперь умножьте число под чертой и запишите результат под числителем.
Например, для задачи 3/2 x 32/7 умножьте 2 на 7, чтобы получить 14
Шаг 4. Преобразуйте ответы в смешанные дроби, если это возможно
Если числитель произведения больше знаменателя, найдите число, которое дает число, которое приближается к числителю при умножении на знаменатель (позже это число будет действовать как целое). После этого поместите разницу между произведением знаменателя на целое число и числителем над знаменателем, чтобы получить форму смешанного числа.
- Например, если в результате умножения вы получили 96/14, найдите число, которое дает сумму, близкую к 96 при умножении на 14. Это число равно 6, и вы получите 12 как разницу между 14 x 6 и 96. Поставим 12 над знаменателем (14).
- Обычно учитель просит вас написать ответ в той же форме, что и вопрос. Если вы получили смешанное число как проблему, вам также необходимо преобразовать ответ в смешанное число.
Шаг 5. По возможности упростите результаты
Возможно, у вас получатся как целые числа, так и дроби. Посмотрите на дроби и проверьте, можно ли их упростить. Например, если у вас результат 6 12/14, разделите 12/14 на 2, чтобы упростить его до 6/7.
В этом примере задачи ваш окончательный ответ будет 6 6/7
Метод 2 из 2: умножение дробей на целые числа
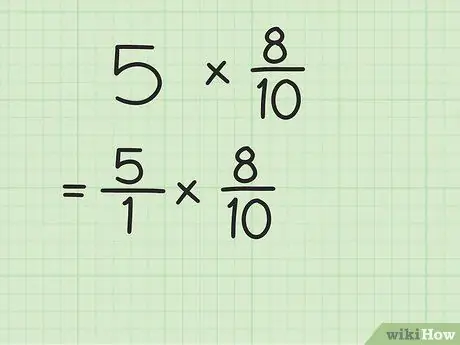
Шаг 1. Перепишите целое число в дробь
Чтобы преобразовать целое число в дробь, просто поместите его над числом 1 (знаменатель). После этого существующие целые числа превратятся в неправильные дроби.
Например, если у вас есть задача 5 x 8/10, поместите 5 над числом 1. Теперь умножение составляет 5/1 x 8/10
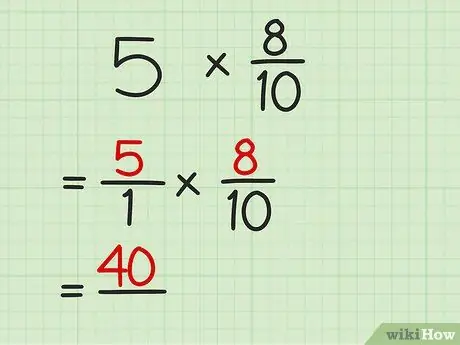
Шаг 2. Умножьте числитель обеих дробей
Помните, что числитель - это число, которое находится над линией. Запишите результат и проведите линию под продуктом.
Например, в задаче 5/1 x 8/10 умножьте 5 на 8, чтобы получить 40
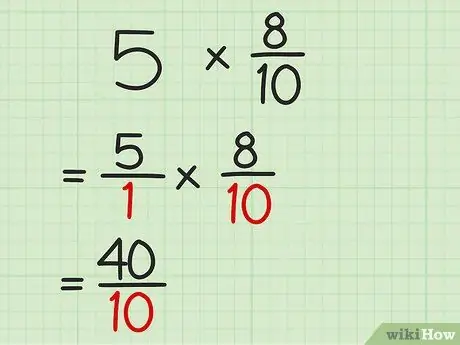
Шаг 3. Умножьте знаменатели обеих дробей
На этом этапе вы можете умножить числа под линией, чтобы получить знаменатель продукта. Теперь у вас есть ответ на умножение в виде дроби.
Например, для задачи 5/1 x 8/10 умножьте 1 на 10, чтобы получить 10. Поместите число под чертой, чтобы произведение двух дробей было 40/10
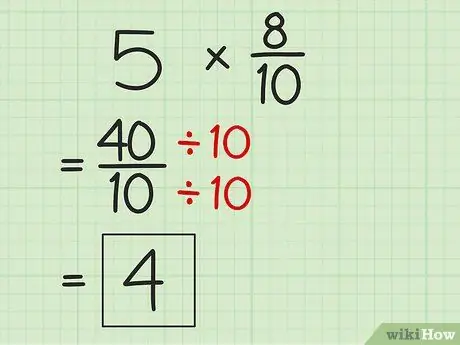
Шаг 4. Если возможно, сверните ответы
Поскольку продукт продукта может быть неправильной дробью, упростите результат до наименьшего размера. Разделите числитель на знаменатель, чтобы получить более простой результат.
- Чтобы упростить 40/10, разделите 40 на 10, чтобы получить 4 как новый ответ на задачу умножения.
- Обычно вы получаете смешанные числа, потому что в результате деления будет остаток.
