Разделить дроби на целые числа не так сложно, как кажется. Чтобы разделить дробь на целое, все, что вам нужно сделать, это преобразовать целое число в дробь, найти обратную дробь и умножить результат на первую дробь. Если вы хотите знать, как это сделать, просто выполните следующие действия:
Шаг
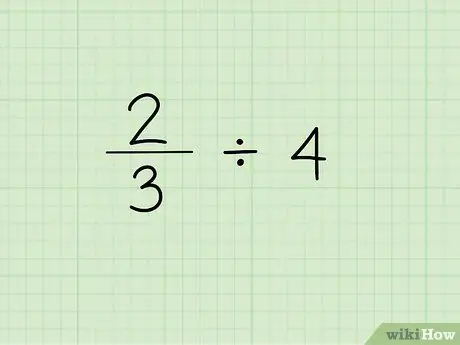
Шаг 1. Запишите проблему
Первый шаг к делению дроби на целое число - записать дробь, за которой следует знак деления и целое число, необходимое для деления дроби. Допустим, мы работаем со следующей проблемой: 2/3 4.
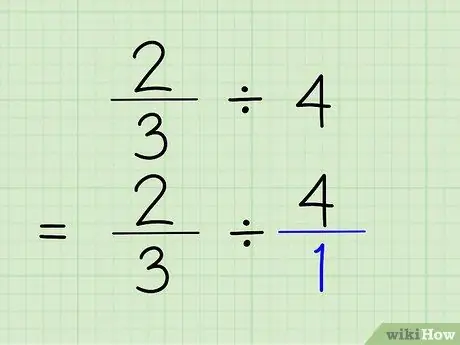
Шаг 2. Преобразуйте целые числа в дроби
Чтобы преобразовать целое число в дробь, все, что вам нужно сделать, это поместить целое число над числом 1. Целое число становится числителем, а 1 становится знаменателем дроби. Сказать 4/1 на самом деле то же самое, что сказать 4, потому что вы показываете, что число содержит «1» только 4 раза. Проблема будет 2/3 4/1.
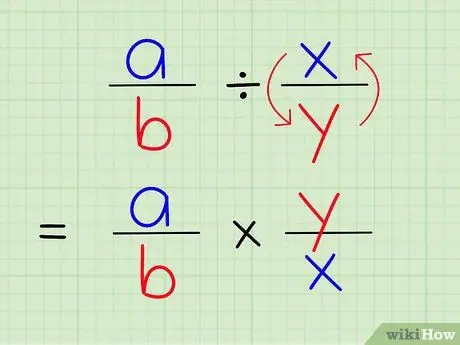
Шаг 3. Деление одной дроби на другую равносильно умножению этой дроби на обратную величину другой дроби
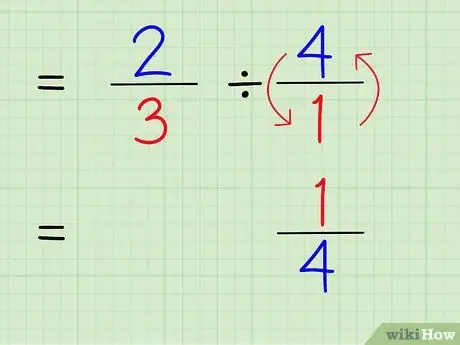
Шаг 4. Напишите обратное от целого числа
Чтобы найти обратное число, поменяйте местами числитель и знаменатель числа. Поэтому, чтобы найти величину, обратную 4/1, просто поменяйте местами числитель и знаменатель, чтобы число стало 1/4.
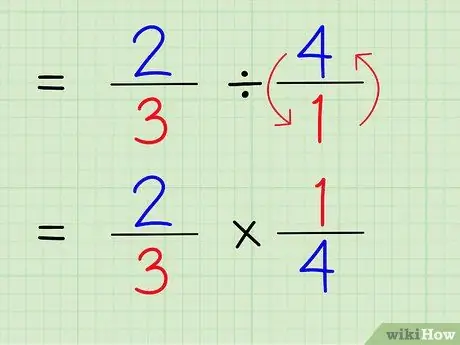
Шаг 5. Измените знак деления на знак умножения
Задача будет 2/3 х 1/4.
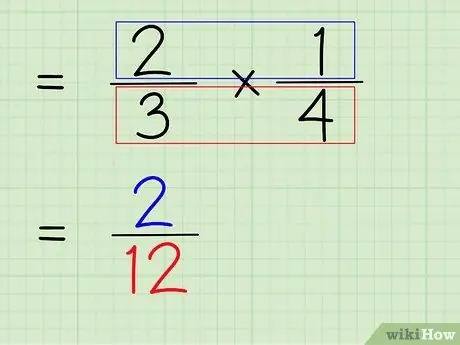
Шаг 6. Умножьте числитель и знаменатель дроби
Итак, следующий шаг - умножить числитель и знаменатель дроби, чтобы получить новый числитель и знаменатель в качестве окончательного ответа.
- Чтобы умножить числители, просто умножьте 2 x 1, чтобы получить 2.
- Чтобы умножить знаменатели, просто умножьте 3 x 4, чтобы получить 12.
- 2/3 х 1/4 = 2/12
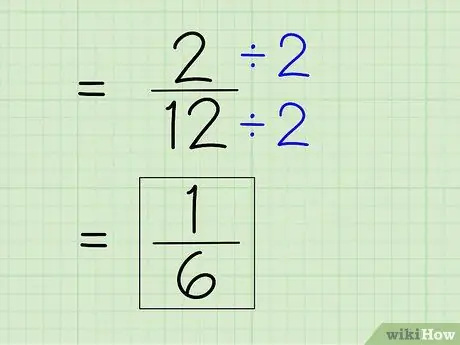
Шаг 7. Упростите дробь
Чтобы упростить дробь, вы должны найти наименьший знаменатель, что означает, что вы должны разделить числитель и знаменатель на любое число, которое делит оба числа. Поскольку 2 является числителем, вам нужно будет проверить, может ли 2 полностью разделить 12 - это возможно, потому что 12 - четное число. Затем разделите числитель и знаменатель на 2, чтобы получить новый числитель и знаменатель, чтобы получить простой ответ.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- Дробь 2/12 может быть упрощена до 1/6. Это ваш окончательный ответ.
подсказки
- Это сделано для помощи памяти, это простой способ запомнить, как производить все эти вычисления. Имейте в виду: «Дроби легко делить, второе число переставлять и умножать!»
- Другой вариант вышеупомянутого метода - JGB / JBG. Не меняйте первое число. Перейти к умножению. Поменяйте местами последнее число. Или сначала B, затем G.
- Если вы отмените вычисление до того, как умножите его, вам может не понадобиться находить простейшую форму дроби, потому что результат уже находится в простейшей форме дроби, как вы можете видеть. В нашем примере, прежде чем мы умножим 2/3 × 1/4, мы увидим, что первый числитель (2) и второй знаменатель (4) имеют одинаковый множитель 2, который мы можем отменить, прежде чем продолжить вычисление. Это преобразует задачу в 1/3 × 1/2, что дает немедленный результат 1/6 и экономит время, упрощая дробь на более позднем этапе.
- Если одна из ваших дробей отрицательная, этот метод все еще работает; убедитесь, что вы отслеживаете знаки при выполнении этих шагов.
