- Автор Jason Gerald [email protected].
- Public 2023-12-16 11:35.
- Последнее изменение 2025-01-23 12:44.
Квадратный корень из числа легко найти, если ответ будет целым числом. Если ответ не является целым числом, вы можете выполнить ряд процессов, чтобы получить квадратный корень, даже если вы не используете калькулятор. Для этого вам нужно понимать основы умножения, сложения и деления.
Шаг
Метод 1 из 3: поиск квадратного корня целого числа
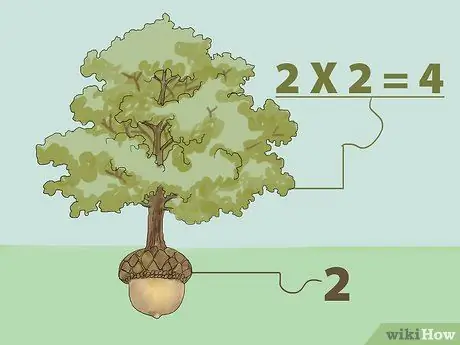
Шаг 1. Найдите точный квадратный корень путем умножения
Квадратный корень числа - это число, которое при умножении само на себя возвращает исходное число. Другими словами: «Какое число мы можем умножить само на себя, чтобы получить желаемое число?»
- Например, квадратный корень из 1 равен 1, потому что 1, умноженное на 1, равно 1 (1X1 = 1). Таким образом, квадратный корень из 4 равен 2, потому что 2, умноженное на 2, дает 4 (2X2 = 4). Думайте о концепции квадратного корня как о дереве. Дерево растет из семян. Итак, дерево больше семени, которое вырастает из семени, которое является его корнем. В приведенном выше примере 4 - это дерево, а 2 - семя.
- Итак, квадратный корень из 9 равен 3 (3X3 = 9), из 16 равен 4 (4X4 = 16), из 25 равен 5 (5X5 = 25), из 36 равен 6 (6X6 = 36), из 49 равен 7 (7X7 = 49), из 64 - 8 (8X8 = 64), из 81 - 9 (9X9 = 81), а из 100 - 10 (10X10 = 100).
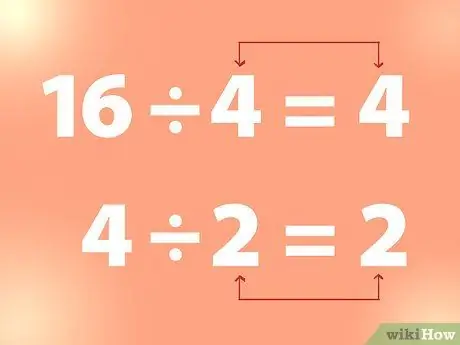
Шаг 2. Используйте непрерывное деление, чтобы найти квадратный корень
Чтобы найти квадратный корень из целого числа, вы можете разделить целое число на число, пока не получите число, равное делителю.
- Пример: 16, разделенное на 4, равно 4. А 4, разделенное на 2, равно 2, и так далее. Таким образом, из приведенного выше примера 4 - это квадратный корень из 16, а 2 - это квадратный корень из 4.
- В совершенных квадратных корнях нет дробей или десятичных знаков, потому что они целые числа.
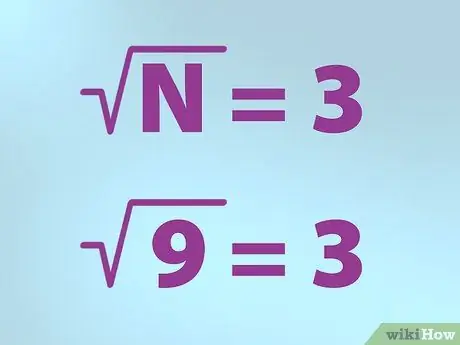
Шаг 3. Используйте правильный символ для квадратного корня
Математики используют специальный символ для обозначения квадратного корня. Форма похожа на галочку с плюсом вверху справа.
- N равно числу, для которого вы хотите найти квадратный корень. N ставится под галочкой.
- Итак, если вы хотите найти квадратный корень из 9, напишите формулу, поставив «N» (9) внутри галочки (символ «корень»), затем поставьте знак равенства и затем 3. Это означает «квадратный корень из 9 равно 3 ".
Метод 2 из 3: поиск квадратного корня другого числа
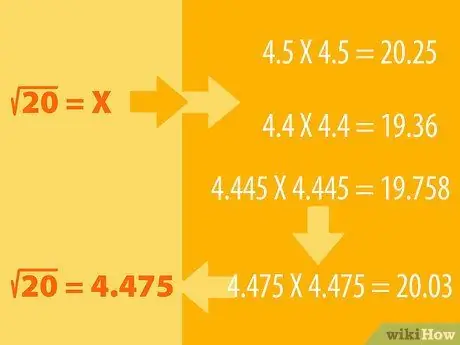
Шаг 1. Угадайте и выполните процесс исключения
Трудно найти квадратный корень из нецелого числа. Однако это не значит, что это невозможно.
- Например, вы хотите найти квадратный корень из 20. Мы знаем, что 16 - это полный квадрат, квадратный корень которого равен 4 (4X4 = 16). Тогда 25 квадратных корней равны 5 (5X5 = 25), поэтому квадратный корень из 20 должен лежать между ними.
- Вы можете догадаться, что квадратный корень из 20 равен 4,5. Теперь возведите в квадрат 4,5, чтобы увидеть результат. То есть мы умножаем 4, 5 на себя: 4, 5X4, 5. Посмотрите, будет ли ответ больше или меньше 20. Если ваше предположение слишком велико, попробуйте другое число (например, 4, 6 или 4, 4) и скорректируйте угадывай соответственно, пока не получишь число 20.
- Например, 4, 5X4, 5 = 20, 25, поэтому по логике мы должны найти меньшее число, может быть, 4, 4. 4, 4X4, 4 = 19, 36. Итак, квадратный корень из 20 должен лежать между 4, 5 и 4, 4. Попробуйте с 4, 445X4, 445. Результат - 19, 758. Результат приближается. Продолжайте пробовать с другими числами, пока не получите 4, 475X4, 475 = 20, 03. Округляя вверх, это число равно 20.

Шаг 2. Используйте процесс усреднения
Этот процесс также начинается с нахождения двух ближайших идеальных квадратов, окруженных числом.
- Затем разделите это число на один из точных квадратных корней. Возьмите ответ, а затем найдите среднее значение между этим числом и числом, от которого вы хотите найти корень (среднее можно найти, сложив два вместе и разделив на два). Затем разделите исходное число на полученное среднее значение. На последнем шаге найдите среднее значение результатов, среднее значение которого рассчитывается в первый раз.
- Звучит сложно? Было бы проще, если бы привести пример. Например, 10 находится между двумя точными квадратами 9 (3x3 = 9) и 16 (4X4 = 16). Квадратные корни обоих чисел равны 3 и 4. Итак, разделите 10 на первое число 3. Результат - 3, 33. Теперь найдите среднее значение 3 и 3, 33, сложив их вместе и разделив на 2. Результат равно 3, 1667 Теперь разделите 10 на 3,1667. Результат будет 3,1579. Затем найдите среднее значение 3,1579 и 3,1667, сложив их и разделив на 2. Результат: 3,1623.
- Проверьте свой результат, умножив ответ (в этом примере 3, 1623) на себя. Результат 3,1623, умноженный на 3,1623, получается 10,001.
Метод 3 из 3: возведение отрицательных чисел в квадрат
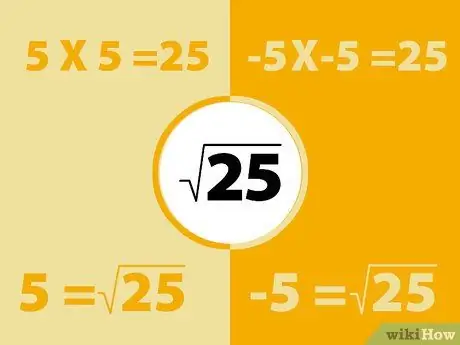
Шаг 1. Возведите отрицательные числа в квадрат, используя тот же метод
Помните, что отрицательное умножение на отрицательное - положительное. Итак, квадрат отрицательного числа даст положительное число.
- Например, -5X-5 = 25. Однако также помните, что 5x5 = 25. Таким образом, квадратный корень из 25 может быть -5 или 5. Обычно каждое число имеет два квадратных корня.
- Точно так же 3X3 = 9 и -3X-3 = 9, поэтому квадратные корни из 9 равны 3 и -3. Положительный квадратный корень называется «главным корнем». На данный момент нам просто нужно обратить внимание на этот ответ.
Шаг 2. Воспользуйтесь калькулятором
Хотя лучше уметь вычислять вручную, существует множество онлайн-калькуляторов для вычисления квадратных корней.
- Найдите кнопку извлечения квадратного корня на обычном калькуляторе.
- В онлайн-калькуляторе введите непосредственно число, для которого вы хотите найти значение квадратного корня, и нажмите кнопку. Компьютер покажет вам значение квадратного корня.
подсказки
-
Всегда помните о нескольких важных идеальных квадратах:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Также помните этот идеальный квадрат: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Также обратите внимание на это: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






