- Автор Jason Gerald [email protected].
- Public 2024-01-19 22:14.
- Последнее изменение 2025-06-01 06:07.
Вычитание - это просто вычитание одного числа из другого. Вычесть одно целое число из другого легко, но при вычитании дробей или десятичных дробей вычитание может оказаться сложным. Как только вы поймете, что такое вычитание, вы сможете использовать более сложные математические концепции и сможете легче складывать, умножать и делить числа.
Шаг
Метод 1 из 6: вычитание больших целых чисел заимствованием

Шаг 1. Запишите большое число
Например, вы хотите решить 32 - 17. Сначала запишите 32.

Шаг 2. Напишите меньшее число прямо под ним
Убедитесь, что вы поместили значения десятков и единиц в правильные столбцы, так, чтобы 3 из 32 находились прямо над 1 из 17, а 2 из 32 - прямо над 7 из 17.
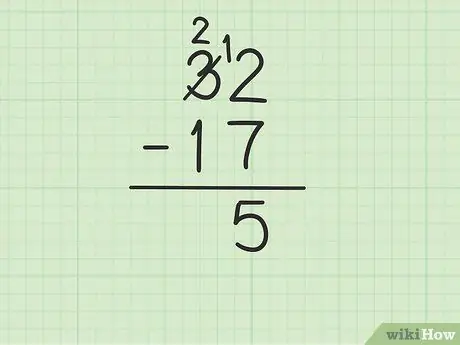
Шаг 3. Вычтите верхнее число в столбце единиц из числа внизу
Однако это может усложниться, если нижнее число больше верхнего числа. В этом случае 7 больше 2. Вот что вам нужно сделать:
- Чтобы превратить 2 в 12, нужно заимствовать из числа 3 из 32 (также известного как группировка).
- Вычеркните цифру 3 из 32 и замените ее цифрой 2, при этом цифра 2 станет 12.
- Теперь вы можете вычесть 12-7, что равно 5. Напишите 5 под двумя числами, которые вы вычитаете, чтобы они оказались в столбце единиц новой строки.
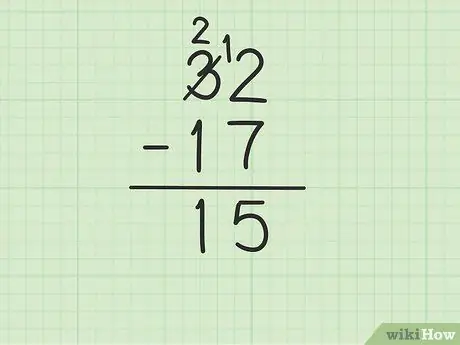
Шаг 4. Вычтите верхнее число в столбце десятков из нижнего числа
Помните, что 3 превратилось в 2. Теперь вычтите 1 из 17 из 2 выше, чтобы получить (2-1) 1. Напишите 1 ниже, в столбце десятков, слева от 5 в столбце единиц. Вы пишете 15. То есть 32 - 17 = 15.
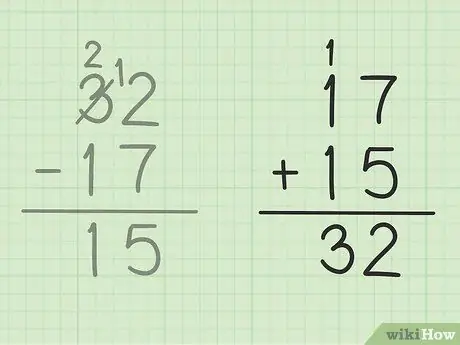
Шаг 5. Проверьте свою работу
Если вы хотите убедиться, что вы вычли два числа правильно, все, что вам нужно сделать, это сложить свой ответ с меньшим числом, чтобы получить большое число. В этой задаче вам нужно добавить свой ответ 15 к меньшему числу вычитания 17. 15 + 17 = 32, чтобы ваш ответ был правильным. Безопасно!
Метод 2 из 6: вычитайте маленькие целые числа
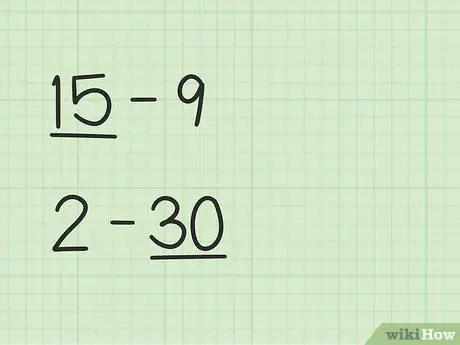
Шаг 1. Найдите большее число
Такие задачи, как 15-9, будут выполняться иначе, чем 2-30.
- В вопросах 15-9 первое число 15 больше второго числа 9.
- В вопросах 2-30 второе число 30 больше первого числа 2.
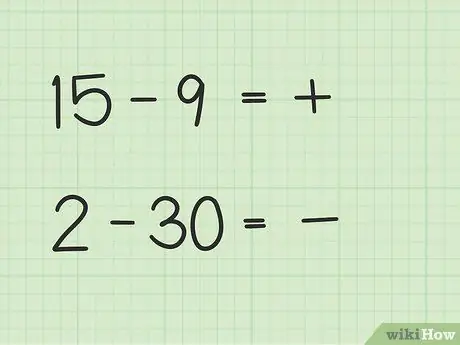
Шаг 2. Решите, будет ли ваш ответ положительным или отрицательным
Если первое число больше, ответ положительный. Если второе число больше, ответ отрицательный.
- На первый вопрос, 15-9, ваш ответ положительный, потому что первое число больше второго.
- На второй вопрос от 2 до 30 ваш ответ отрицательный, потому что второе число больше первого.
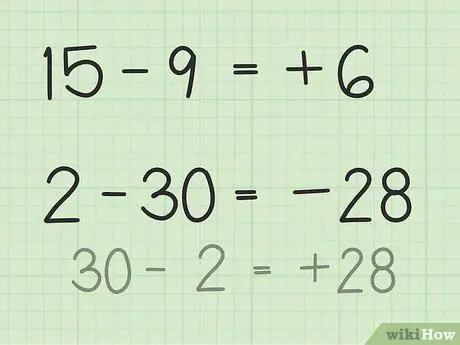
Шаг 3. Найдите разницу между двумя числами
Чтобы вычесть два числа, вы должны представить себе разницу между двумя числами и вычислить числа между ними.
- Для вопросов 15-9 представьте себе стопку из 15 покерных фишек. Выбросьте 9 фишек и только 6. Итак, 15 - 9 = 6. Вы также можете представить числовую линию. Подумайте о числах от 1 до 15, затем сбросьте или верните 9 единиц, чтобы получить 6.
- Для вопросов 2-30 самый простой способ решить эту проблему - перевернуть число и сделать результат отрицательным после вычитания. Итак, 30 - 2 = 28, поэтому разница между 28 и 30 равна 2. Теперь сделайте результат отрицательным, потому что вы уже определили, что ответ отрицательный, потому что второе число больше первого. Итак, 2-30 = -28.
Метод 3 из 6: вычитание десятичных знаков
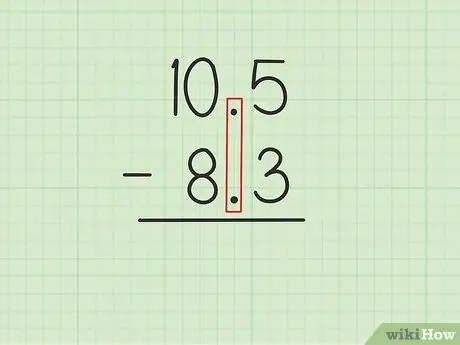
Шаг 1. Запишите большее число над меньшим, выровняв десятичные точки
Предположим, вы хотите решить следующие задачи: 10, 5 - 8, 3. Запишите 10, 5 вместо 8, 3 так, чтобы десятичные точки двух чисел были параллельны., 5 из 10, 5 должны быть непосредственно выше, 3 из 8, 3 и 0 из 10, 5 должны быть выше 8 из 8, 3.
Если у вас возникла проблема из-за того, что два числа не имеют одинакового числа после десятичной точки, записывайте 0 в поле, пока сумма чисел не станет одинаковой. Например, задача 5, 32 - 4, 2, вы можете записать ее как 5, 32 - 4, 2 0. Это не изменит значение второго числа, но упростит вычитание двух чисел.

Шаг 2. Вычтите верхнее число в столбце десятков из числа ниже
В этом случае вам нужно вычесть 3 из 5. 5 - 3 = 2, поэтому вы должны написать 2 под 3 из 8, 3.
Убедитесь, что вы поставили десятичную точку в ответ, чтобы было написано: 2

Шаг 3. Вычтите число над столбцом единиц из числа под ним
Вы должны вычесть 8 из 0. Заимствовать 1 из части десятков, чтобы изменить 0 до 10, и вычесть 10-8, чтобы получить 2. Вы также можете считать 10-8 без заимствования, потому что во втором столбце десятков нет чисел. Напишите ответ под цифрой 8 слева от десятичной точки.

Шаг 4. Запишите окончательный результат
Ваш окончательный результат - 2, 2.

Шаг 5. Проверьте свою работу
Если вы хотите убедиться, что ваше десятичное вычитание правильно, все, что вам нужно сделать, это сложить свой ответ с меньшим числом, чтобы получить большее число. 2, 2 + 8, 3 = 10, 5, так что вы закончили.
Метод 4 из 6: вычесть дроби

Шаг 1. Совместите знаменатель и числитель дроби
Допустим, вы хотите решить задачи 13/10 - 3/5. Запишите задачу так, чтобы два числителя 13 и 3 и два знаменателя 10 и 5 были расположены напротив друг друга. Эти два числа разделены знаком вычитания. Это поможет вам визуализировать проблему и легче ее решить.

Шаг 2. Найдите наименьший общий знаменатель
Наименьший общий знаменатель - это наименьшее число, которое можно разделить на два числа. В этом примере вам нужно найти наименьший общий знаменатель, который делится на 10 и 5. Вы обнаружите, что 10 - это наименьший общий знаменатель для обоих чисел, потому что 10 делится на 10 и 5.
Обратите внимание, что наименьший общий знаменатель двух чисел не всегда является одним из них. Например, наименьший общий знаменатель для 3 и 2 равен 6, потому что 6 - это наименьшее число, которое можно разделить на два числа
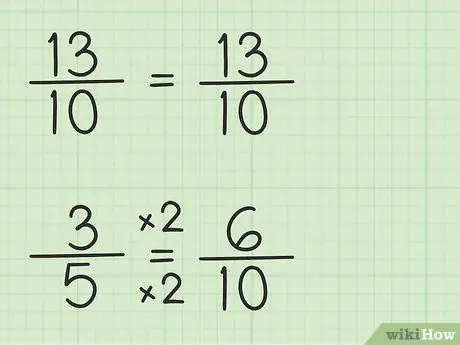
Шаг 3. Запишите дроби, используя тот же знаменатель
Дробь 13/10 может быть записана таким же образом, потому что знаменатель равен 10, наименьший общий знаменатель, который равен 10, умноженному на 1. Однако дробь 3/5 должна быть переписана, потому что знаменатель равен 5, наименьшему общему знаменателю., что составляет 10, умноженное на 2. Итак, дробь 3/5 должна быть умножена на 2/2, чтобы знаменатель стал равен 10, так что 3/5 x 2/2 = 6/10. Вы нашли эквивалентную дробь. 3/5 эквивалентно 6/10, хотя 6/10 позволяет вычесть первое число, 13/10.
Напишите новый вопрос вроде этого: 13/10 - 6/10
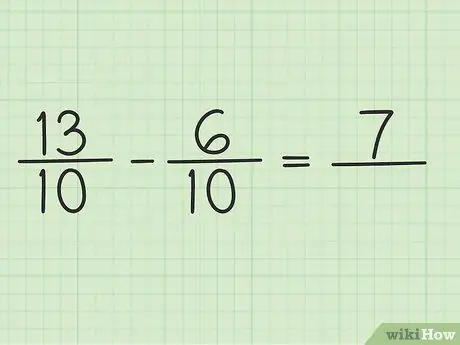
Шаг 4. Вычтите числитель до двух чисел
Просто вычтите 13-6, чтобы получить 7. Знаменатель дроби изменить нельзя.
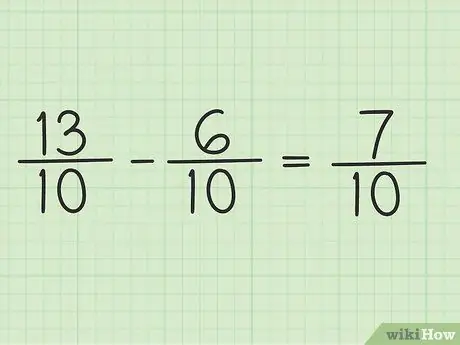
Шаг 5. Запишите новый числитель над тем же знаменателем, чтобы получить окончательный результат
Новый числитель 7. Обе дроби имеют знаменатель 10. Ваш окончательный результат - 7/10.
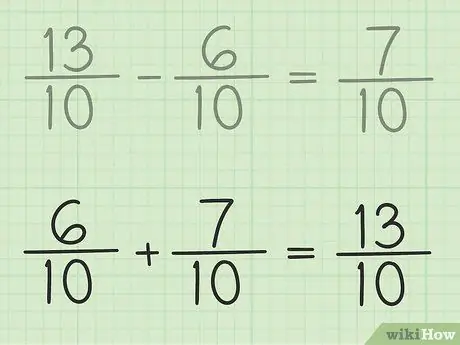
Шаг 6. Проверьте свою работу
Если вы хотите убедиться, что вы правильно вычитаете дробь, просто сложите свой ответ и меньшую дробь, чтобы в результате получилась большая дробь. 7/10 + 6/10 = 13/10. С этим покончено.
Метод 5 из 6: вычитание дробей из целых чисел

Шаг 1. Запишите проблему
Например, предположим, что вы хотите решить следующую задачу: 5 -. Запиши это.
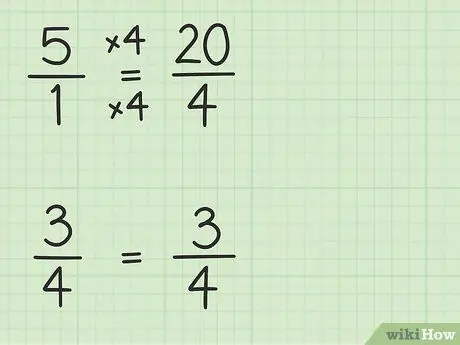
Шаг 2. Преобразуйте целые числа в дроби, имеющие тот же знаменатель, что и другие дроби
Вы будете преобразовывать 5 в дробь со знаменателем 4, чтобы можно было вычесть два числа. Поэтому вам нужно думать о 5 как о доле 5/1. Затем вы можете умножить числитель и знаменатель новой дроби на 4, чтобы знаменатели двух чисел совпадали. Итак, 5/1 x 4/4 = 20/4. Эта дробь равна 5, но позволяет вычесть два числа.
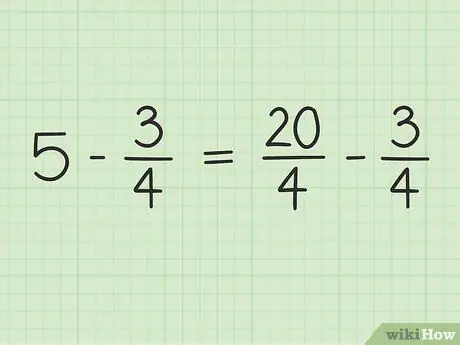
Шаг 3. Перепишите задачу
Новую задачу можно записать так: 20/4 - 3/4.
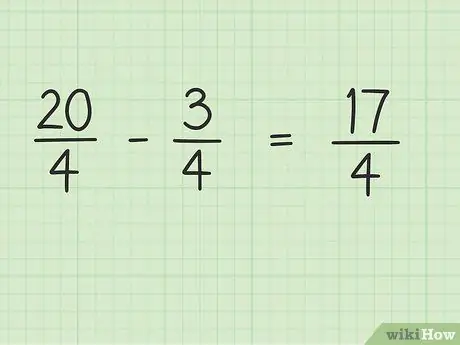
Шаг 4. Вычтите числитель дроби, при этом знаменатель останется прежним
Теперь просто вычтите 20 на 3, чтобы получить окончательный результат. 20 - 3 = 17, поэтому 17 - новый числитель. Знаменатель можно оставить прежним.
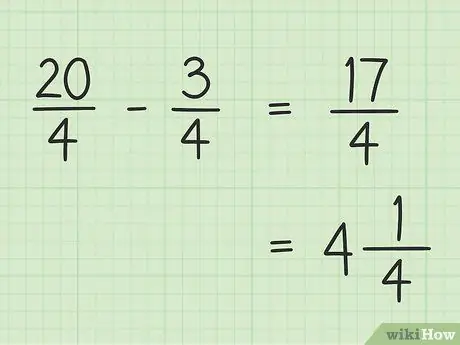
Шаг 5. Запишите окончательный результат
Ваш окончательный результат - 17/4. Если вы хотите записать это как смешанное число, разделите 17 на 4, чтобы результат был 4, а остаток - 1, чтобы ваши окончательные 17/4 равнялись 4.
Метод 6 из 6: вычитание переменных
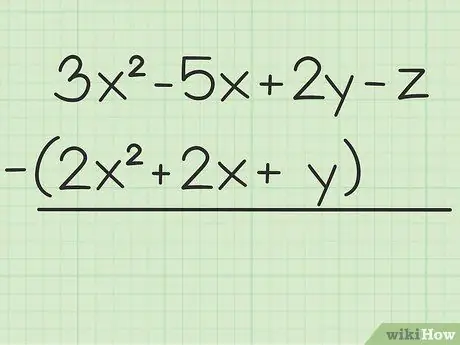
Шаг 1. Запишите проблему, которую хотите решить
Например, следующий вопрос: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Запишите первый набор переменных поверх второго.
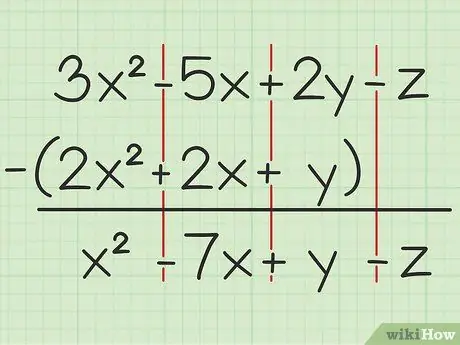
Шаг 2. Вычтите те же переменные
Если вы встретите переменную, вы можете добавить или вычесть только ту же переменную, которая записана с той же степенью квадрата. Это означает, что вы можете вычесть 4x2 от 7x2, но не может вычесть 4x из 4y. Итак, вы можете разбить проблему следующим образом:
- 3x2 - 2x2 = х2
- -5x - 2x = -7x
- 2у - у = у
- -z - 0 = -z
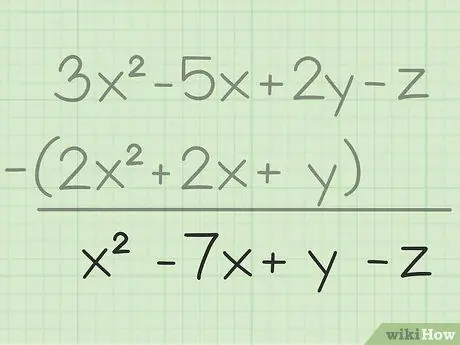
Шаг 3. Запишите окончательный результат
Вы вычли все те же переменные, все, что вам нужно сделать, это написать окончательный результат, который будет содержать все вычтенные вами переменные. Вот конечный результат:






