- Автор Jason Gerald [email protected].
- Public 2023-12-16 11:35.
- Последнее изменение 2025-01-23 12:44.
Для большинства людей дроби - это первые сложные вычисления, с которыми приходится сталкиваться. Понятие дробей довольно сложное и требует для этого изучения особых условий. Поскольку у дробей есть особые правила сложения, вычитания, умножения и деления, многие люди не понимают этого. Однако, попрактиковавшись, любой может выучить и выполнить вычисления, связанные с дробями.
Шаг
Метод 1 из 5: понимание дробей
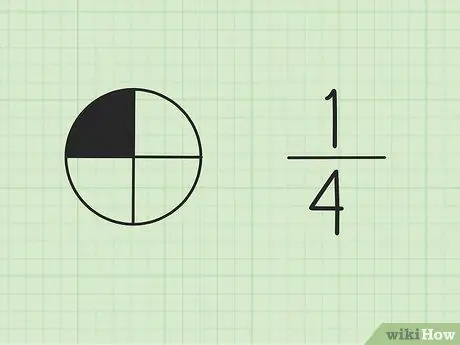
Шаг 1. Поймите, что дроби являются частью целого
Число вверху называется числителем и представляет собой количество частей общей суммы. Число внизу называется знаменателем, который представляет общее количество частей.
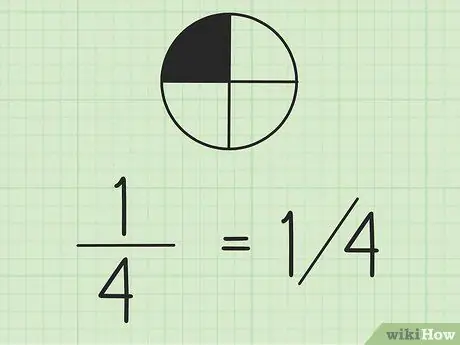
Шаг 2. Помните, что дроби можно записывать с помощью слэшей
Число слева - числитель, а число справа - знаменатель. Если вы работаете с дробями в одной строке, рекомендуется написать числитель над знаменателем.
Например, если вы возьмете один из четырех кусочков пиццы, у вас получится пицца. Если у вас 7/3 пиццы, это означает, что у вас есть две целые пиццы плюс 1 из 3 кусочков пиццы
Метод 2 из 5: разница между смешанными и простыми дробями

Шаг 1. Помните, что смешанные числа состоят из целых чисел и дробей, например 2 1/3 или 45 1/2
Обычно вам нужно преобразовать смешанные числа в более простую форму, чтобы сложить, вычесть, умножить или разделить.

Шаг 2. Измените смешанное число, умножив целое число на знаменатель дроби, а затем прибавив его к числителю
Результат записываем в числитель, знаменатель при этом не меняется.
Например, чтобы преобразовать 2 1/3 в простую дробь, умножьте 2 на 3, затем добавьте 1 и получите 7/3

Шаг 3. Преобразуйте простые дроби в смешанные числа, разделив числитель на знаменатель
Весь результат деления записывается как целое число, а остаток деления записывается как числитель дроби. Знаменатель не меняется.
Например, чтобы преобразовать 7/3 в смешанное число, разделите 7 на 3, чтобы получить 2 с остатком 1. Таким образом, смешанное число равно 2 1/3. Простые дроби можно преобразовать в смешанные числа только в том случае, если числитель больше знаменателя
Метод 3 из 5: сложение и вычитание дробей
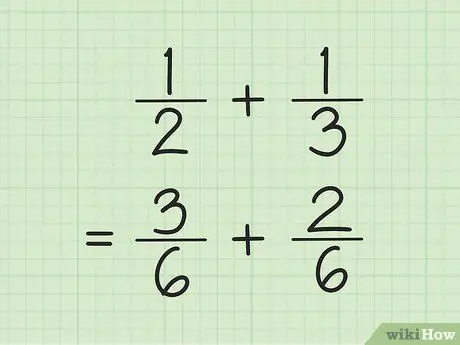
Шаг 1. Найдите общий знаменатель для сложения и вычитания дробей
Уловка состоит в том, чтобы умножить числа в знаменателе, а затем умножить каждый числитель на число, используемое для нахождения знаменателя. Иногда можно найти НОК (наименьшее общее кратное) знаменателя, умножив знаменатели друг на друга.
Например, чтобы сложить и 1/3, сначала найдите НОК (наименьшее общее кратное) двух знаменателей, умножая друг друга. Таким образом, вы умножаете 2 и 3, чтобы получить НОК 6. Умножьте 1 на 3, чтобы получить 3 в качестве нового числителя первой дроби. Умножьте 1 на 2, чтобы получить 2 в качестве нового числителя второй дроби. Ваши новые дроби - 3/6 и 2/6
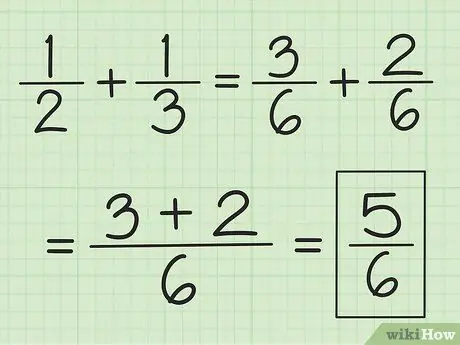
Шаг 2. Сложите два числителя вместе, не меняя знаменатель
Например, 3/6 плюс 2/6 равно 5/6, а 2/6 плюс 1/6 - 3/6
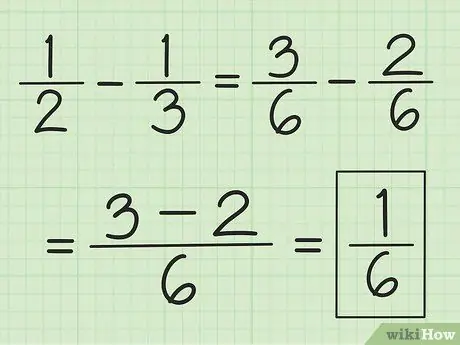
Шаг 3. Используйте аналогичную технику вычитания
Сначала найдите НОК знаменателей, но вместо того, чтобы складывать их, вычтите число первого числителя на число второго.
Например, чтобы вычесть 1/3 из 1/2, сначала измените дроби на 3/6 и 2/6, затем вычтите 3 на 2, чтобы получить 1. В результате получится 1/6
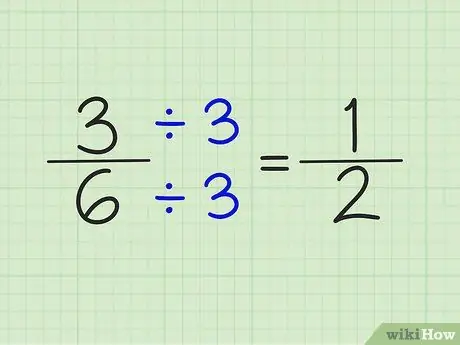
Шаг 4. Упростите дроби, разделив числитель и знаменатель на одно и то же число
Например, число 5/6 не может быть упрощено. Однако 3/6 можно упростить, разделив числитель и знаменатель на число 3. В результате получится дробь 1/2

Шаг 5. Преобразуйте дробь в смешанное число, если числитель больше знаменателя
Метод 4 из 5: умножение и деление дробей
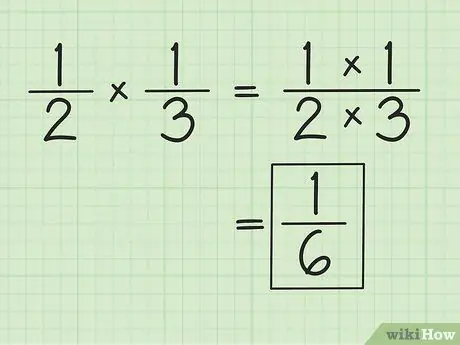
Шаг 1. Умножьте числитель и знаменатель отдельно, чтобы умножить дроби
Например, при умножении на 1/3 результат будет 1/6 (1 умножить на 1 и 2 умножить на 3). При умножении дробей не нужно совпадать знаменатели. При необходимости упростите или измените полученные результаты
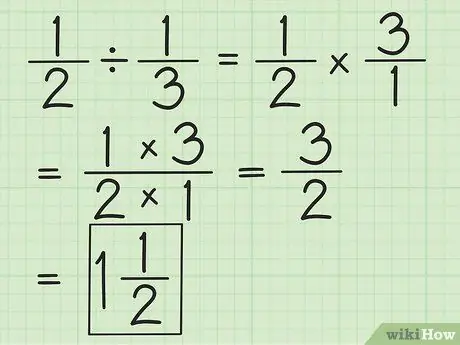
Шаг 2. Разделите две дроби, инвертировав вторую дробь, а затем умножив обе
Например, если вы хотите разделить 1/2 на 1/3, сначала измените вторую дробь на 3/1. Умножьте на 3/1 и получите 3/2. По возможности упростите дроби или преобразуйте их в смешанные числа
Метод 5 из 5: Работа со сложными дробями
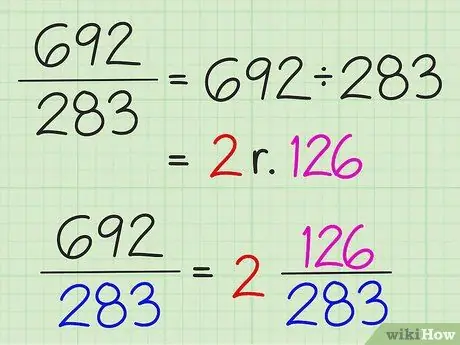
Шаг 1. Работайте со всеми дробями одинаково, даже если задача кажется очень сложной
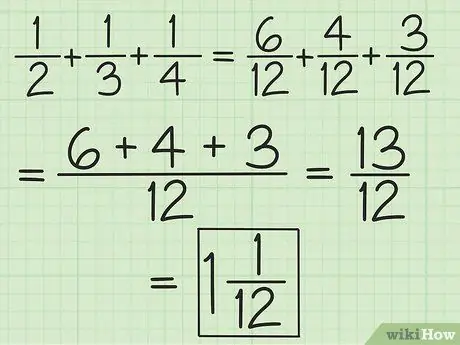
Шаг 2. Сопоставьте знаменатели для всех дробей или работайте в парах, начиная слева направо, чтобы складывать и вычитать более двух дробей
Например, чтобы сложить 1/2, 1/3 и 1/4, вы можете изменить их на 6/12, 4/12 и 3/12, чтобы получить 13/12, или вы можете добавить 3/6 и 2. / 6, чтобы получить 5/6, затем сложите 5/6 и 1/4 (выровняйте знаменатели, чтобы вторая дробь стала 3/12), чтобы получить 13/12 (10/12 плюс 3/12). Преобразуйте его в смешанное число, равное 1 1/12
подсказки
- Помните, что вы выучили много математики. Математика похожа на язык, который вы можете свободно произносить, и теперь вы пытаетесь научиться читать и писать на нем.
- Не забывайте всегда упрощать конечный результат ваших вычислений, независимо от того, является ли ваша задача в форме обыкновенной дроби, смешанного числа или сложной дроби.






