- Автор Jason Gerald [email protected].
- Public 2023-12-16 11:35.
- Последнее изменение 2025-01-23 12:44.
Если вы уже поняли, преобразовать обыкновенные дроби в десятичные не сложно. Чтобы преобразовать обычные дроби в десятичные, вы можете использовать длинное деление, умножение или даже калькулятор, если вы не хотите вычислять вручную. Освоив этот метод, вы сможете легко переводить дроби в десятичные.
Шаг
Метод 1 из 4: с длинным делением
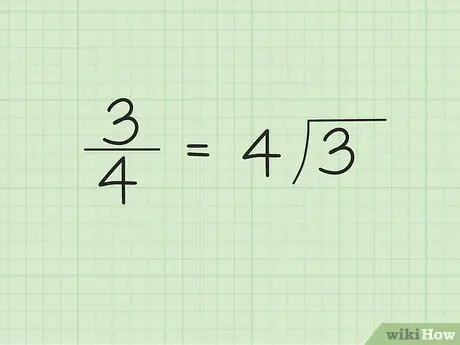
Шаг 1. Запишите знаменатель снаружи / слева от символа делителя и числитель внутри / справа от символа делителя
Например, предположим, что мы хотим преобразовать 3/4 в десятичное число. Напишите «4» снаружи / слева от символа делителя и «3» внутри / справа от символа делителя. «4» - это число, которое делится, а «3» - это число, которое делится.

Шаг 2. Напишите «0», а затем десятичную точку (запятую) над символом делителя
Поскольку считается дробь, результат должен быть меньше единицы, поэтому этот шаг очень важен. После этого напишите десятичный знак, а затем «0» после цифры «3» в правой части символа делителя. Даже если «3» равно «3, 0», ноль позволяет разделить «3, 0» на «4».

Шаг 3. Вычислите ответ в столбик
При долгом делении на данный момент десятичный знак можно игнорировать, поэтому вам нужно только вычислить 30, разделенное на 4. Вот как:
- Сначала разделите 3, 0, что считается 30, на 4. Ближайшее 4 к 30 будет 4 x 7 = 28, в результате чего останется 2. Итак, напишите «7» после «0» над делителем и «28» под « 3, 0 дюймов / правая часть символа делителя. Меньше 28 лет напишите «2», остаток от 30 минус 28.
- Затем напишите «0» после «3, 0», чтобы оно превратилось в «3, 00», что можно рассматривать как «300» внутри / справа от символа делителя. Таким образом, 0 можно уменьшить справа от «2», чтобы «20» делилось на «4».
- «20», разделенное на «4», равняется «5». Итак, напишите «5» после «0,7» над символом делителя, чтобы получилось «0,75».

Шаг 4. Напишите окончательный ответ
Итак, «3», разделенное на «4», равняется «0,75». Запишите ответ. Законченный.
Метод 2 из 4: дроби, образующие повторяющиеся десятичные дроби
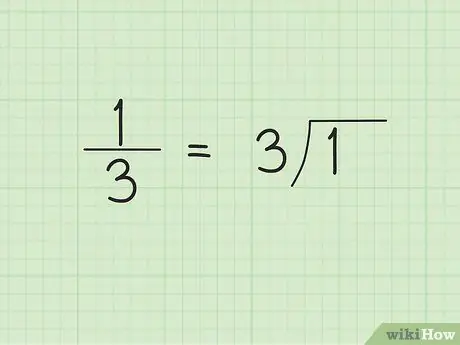
Шаг 1. Сделайте деление в столбик
Когда вы начинаете деление длинных цифр, вы, возможно, не сможете предсказать, что результатом будет повторяющееся десятичное число. Например, предположим, что мы хотим преобразовать обыкновенную дробь 1/3 в десятичную форму. Напишите 3 или знаменатель снаружи / слева от символа делителя и 1 внутри / справа от символа делителя.

Шаг 2. Напишите 0, а затем десятичный знак над символом делителя
Поскольку результат должен быть меньше 1, на этом шаге готовится ответ, который будет записан в десятичной форме. Десятичный знак также должен быть написан справа от числа «1», которое находится справа от символа делителя.
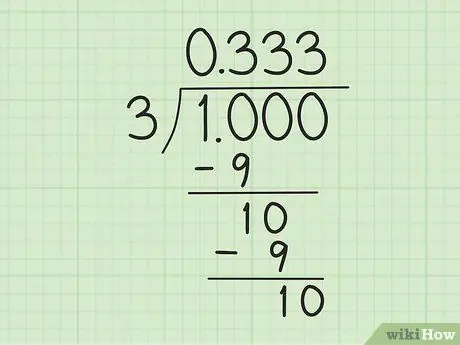
Шаг 3. Начните вычисление деления в столбик
Начните с превращения «1» в «1, 0», которое считается как «10», так что оно делится на «3». Далее выполните следующие действия:
- Разделите 10 на 3. Используйте 3 x 3 = 9, чтобы получить остаток от 1. Итак, напишите 3 справа от «0» над символом делителя и вычтите 10 на 9, чтобы получить остаток от 1.
- Напишите «0» справа от цифры «1» (остаток 10 минус 9 на предыдущем шаге) ниже, чтобы получить еще «10». При повторном делении «10» на «3» тот же процесс повторяется: напишите «3» справа от первой «3» над символом делителя и вычтите новые «10» на «9».
- Продолжайте, пока не сформируется узор. Вы знаете что-то странное? Это разделение может продолжаться вечно. 10 всегда делится на 3: всегда будет «1» внизу и новая «3» после десятичной дроби над символом делителя.
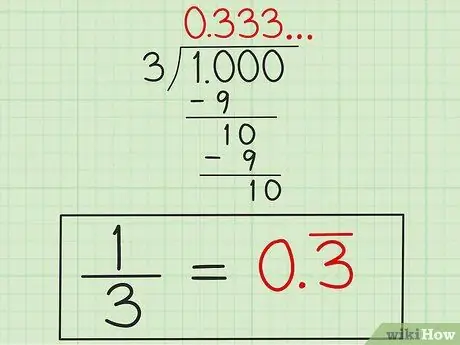
Шаг 4. Напишите ответ
Зная, что цифра «3» будет повторяться, напишите ответ как «0, 3» с линией над цифрой «3» (или «0, 33» с линией над обоими цифрами «3») как указание на то, что цифра «3» продолжает повторяться. Этот ответ представлен в десятичной форме 1/3, потому что 1, деленная на 3, не закончится сама по себе.
Есть много дробей, которые производят повторяющиеся десятичные дроби, например 2/9 («0, 2» с повторением «2»), 5/6 («0, 83» с повторением «3») или 7/9 («0, 7 »с« 7 »повторяется). Этот шаблон всегда возникает, когда знаменатель кратен 3, а числитель не может делиться на знаменатель
Метод 3 из 4: умножением

Шаг 1. Найдите число, которое можно умножить на знаменатель дроби, чтобы получить 10, 100, 1000 или любое другое число с основанием 10
Это может быть простой способ преобразовать дроби в десятичные без использования длинного деления или калькулятора. Во-первых, просто найдите число, которое можно умножить на знаменатель дроби, чтобы получить 10, 100, 1000 и так далее. Для этого сначала разделите 10, затем 100, затем 1000 и так далее на знаменатель, пока не получите целое число. Пример:
- 3/5. 10/5 = 2,2 - целое число. 2 можно умножить на 5, чтобы получить 10. Таким образом, можно использовать 2.
- 3/4. 10/4 = 2, 5. 2, 5 не является целым числом. 100/4 = 25. 25 - целое число. 25 можно умножить на 4, чтобы получить 100. Таким образом, можно использовать 25.
- 5/16. 10/16 = 0, 625, 100/16 = 6, 25, 1000/16 = 62, 5, 10 000/16 = 625. 625 - первое полученное целое число. 625 можно умножить на 16, чтобы получить 10 000. Итак, 625 можно использовать.
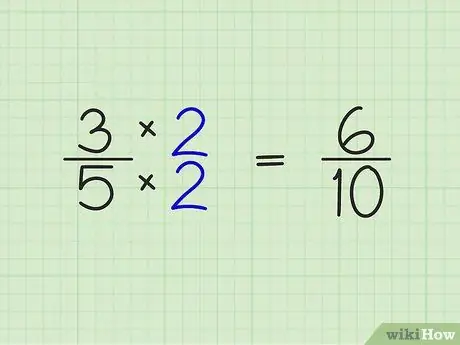
Шаг 2. Умножьте числитель и знаменатель дроби на целое число, полученное на предыдущем шаге
Этот шаг довольно простой. Просто умножьте числа выше и ниже дроби на целое число, полученное на предыдущем шаге. Пример:
- 3/5 х 2/2 = 6/10
- 3/4 х 25/25 = 75/100
- 5/16 х 625/625 = 3,125 / 10000

Шаг 3. Напишите окончательный ответ
Ответ заключается в том, что числитель помечается десятичной дробью в соответствии с количеством нулей в знаменателе. Просто посчитайте, сколько нулей в знаменателе. Если в знаменателе всего 1 0, переместите десятичную запятую влево на 1 цифру и так далее. Пример:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Метод 4 из 4: с помощью калькулятора

Шаг 1. Разделите числитель на знаменатель
Этот метод очень прост. Просто используйте калькулятор, чтобы разделить числитель, число в верхней части дроби, на знаменатель, число в нижней части дроби. Например, вы хотите преобразовать 3/4 в десятичное число. Просто нажмите «3», затем символ деления («÷ '»), затем «4» и, наконец, символ равенства («=»).

Шаг 2. Запишите полученные ответы
Ответ - 0,75. Итак, десятичная форма обыкновенной дроби 3/4 равна 0,75.
подсказки
- Чтобы проверить правильность вашего ответа, умножьте ответ на знаменатель дроби. Если ваш ответ правильный, произведение умножения является числителем дроби.
- Некоторые дроби можно преобразовать в десятичные, создав сопоставимые дроби со знаменателем по основанию 10 (10, 100, 1000 и т. Д.). Затем используйте разрядные значения, чтобы записать правильную десятичную форму.






