- Автор Jason Gerald [email protected].
- Public 2023-12-16 11:35.
- Последнее изменение 2025-01-23 12:44.
Преобразование чисел в проценты, дроби (дроби) и десятичные дроби - важный математический навык. Изучив его, вы поймете, что концепция очень проста. Вы не только научитесь преобразовывать небольшие числа, которые помогут вам при сдаче экзаменов, но также сможете выполнять финансовые / финансовые расчеты.
Шаг
Метод 1 из 3: изменение процента

Шаг 1. Чтобы преобразовать процент в десятичную дробь, переместите десятичный знак на два разряда влево
Если не указано иное, в процентах десятичная точка находится в конце последней цифры. Например, представьте, что 75% на самом деле отображается как 75,0%. Перемещение десятичного знака на два разряда влево преобразует процент в десятичный. Этот метод аналогичен делению числа на 100. Пример:
- 75% изменено на 0,75
- 3,1% изменено на 0,031
- 0,5% изменено на 0,005

Шаг 2. Отобразите процент как долю от 100
Запись числа в виде дроби от 100 - еще один простой способ записать процент. Число процентов - числитель дроби, а 100 - знаменатель. Упростите дробь до ее наименьшего размера.
- Пример: 36% превращается в 36/100.
- Для простоты найдите наибольшее число, которое входит в число 36 и 100. В данном случае это число 4.
- Определите, сколько раз 4 переходит в 36 и 100. Если вы упростите, ответ будет 9/25.
- Чтобы проверить правильность преобразования, разделите 9 на 35 (0, 36) и умножьте на 100 (36%). Это число должно совпадать с исходным процентом.

Шаг 3. Убрать знак процента
Как только процент будет преобразован в десятичную дробь или десятичную дробь, использование знака% становится неприемлемым. Имейте в виду, что процент означает «сотые», поэтому, если вы забудете удалить знак процента после его преобразования (в десятичную или дробную), ваш ответ больше не будет соответствовать сотне.
Метод 2 из 3: преобразование десятичных знаков
Шаг 1. Умножьте десятичную дробь на 100, чтобы преобразовать ее в проценты
Другими словами, переместите десятичную запятую на два разряда вправо. Процент означает «сотые», поэтому десятичная дробь станет «сотыми» после умножения. Не забудьте добавить знак процента / символ (%) после умножения. Например: 0,32 становится 32%, 0,07 становится 7%, 1,25 становится 125%, 0,083 становится 8,3%.

Шаг 2. Преобразуйте конечную десятичную дробь в дробь
Конечное десятичное число - это неповторяющееся десятичное число. Переместите десятичную точку вправо на столько десятичных знаков, сколько есть. Число теперь является числителем дроби. В то время как знаменатель равен 1 с таким количеством нулей, сколько десятичных знаков в исходном числе. В качестве последнего шага упростите дробь.
- Например: 0, 32 имеет два десятичных знака. Переместите десятичную дробь на два разряда вправо и разделите на 100, результат: 32/100. С 4 в качестве общего множителя (числа и знаменателя) дробь может быть упрощена до 8/25.
- Другой пример: 0, 8 имеет только один десятичный знак. Переместите десятичную точку на одну позицию вправо и разделите на 10, результат: 8/10. С 2 в качестве общего множителя дробь может быть упрощена до 4/5.
- Чтобы проверить, вы можете просто разделить полученную дробь и убедиться, что число совпадает с исходной десятичной дробью: 8/25 = 0,32.

Шаг 3. Преобразуйте повторяющиеся десятичные дроби в дроби
Повторяющееся десятичное число - это десятичное число, состоящее из непрерывно повторяющейся серии чисел. Например, если повторяющееся десятичное число - 0, 131313… в этом числе есть 2 повторяющихся десятичных знака (13 повторяется). Определите количество повторяющихся десятичных знаков, затем умножьте десятичную дробь на 10. , где n - количество повторяющихся десятичных знаков.
- Например, 0, 131313… умноженное на 100 (10 в степени 2), и мы получим 13, 131313…
- Чтобы определить числитель (число вверху), вычтите повторяющуюся часть из десятичной дроби. Например, 13, 131313… - 0, 131313… = 13, поэтому числитель равен 13.
- Чтобы определить знаменатель (число ниже), вычтите 1 из числа, которое вы использовали для умножения. Например, 0, 131313… умножается на 100, поэтому знаменатель равен 100 - 1 = 99.
- Конечная дробь для 0, 131313… 13/99.
-
Еще несколько примеров:
- 0, 333… становится 3/9
- 0, 123123123… становится 123/999
- 0, 142857142857… становится 142857/999999
- При необходимости преобразуйте дробь в ее наименьший вид. Например, 142857/999999 становится 1/7.
Метод 3 из 3: преобразование дробей
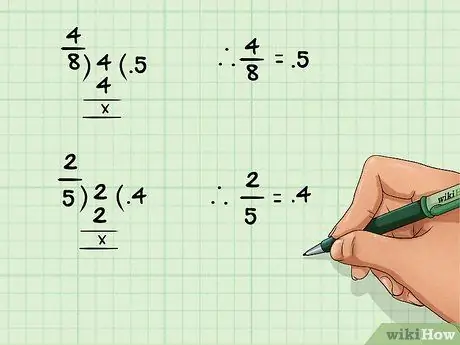
Шаг 1. Разделите числитель на знаменатель, чтобы преобразовать дробь в десятичную дробь
Определите разделительную линию между числителем и знаменателем как «деленное на». Другими словами, любую дробь x / y можно интерпретировать как x, деленное на y.
Например: дробь 4/8 возвращает десятичное число 0,5

Шаг 2. Определите количество десятичных знаков
Многие числа не делятся поровну друг с другом. Если вы разделите его, вы должны определить, сколько десятичных знаков вам нужно, чтобы дать ответ. Часто по умолчанию используется два десятичных знака. При сокращении дроби помните правило округления: если следующее число равно 5, округляйте предыдущее число в большую сторону. Например, 0,145 округляется до 0,15.
- Например: дробь 5/17 возвращает десятичное число 0, 2941176470588…
- Последнее десятичное число можно записать как 0,29.
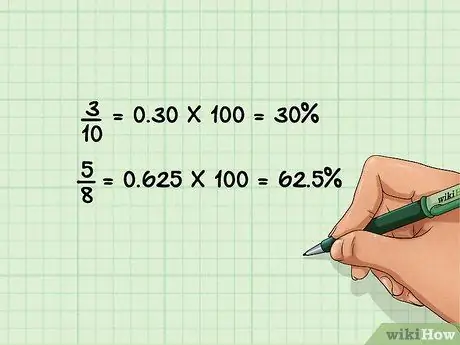
Шаг 3. Разделите дробь, а затем умножьте на 100, чтобы преобразовать ее в проценты
Как и при преобразовании дроби в десятичную дробь, разделите числитель на знаменатель. Умножьте полученное десятичное число на 100 и добавьте символ процента (%), чтобы завершить процесс преобразования.
- Если у вас 4/8, деление 4 на 8 даст вам 0,50, а затем умножение этого числа на 100 даст вам 50. Добавление знака процента (%) дает окончательный ответ 50%.
-
Еще несколько примеров:
- 3/10 = 0, 30 * 100 = 30%
- 5/8= 0, 625 * 100 = 62, 5%
подсказки
- Знание расписания вам очень поможет.
- Помните, что учителя обычно знают, пользовался ли кто-нибудь калькулятором. Если (по правилам) вы не должны использовать калькулятор, вероятно, лучше этого не делать.
- Многие калькуляторы имеют дробную клавишу. Возможно, можно будет использовать калькулятор для уменьшения дробей до их наименьшего размера. Подробнее читайте в инструкции к калькулятору.
Предупреждение
- Убедитесь, что десятичная точка находится в правильном месте.
- При преобразовании дроби в десятичную обязательно делите числитель на знаменатель.






