- Автор Jason Gerald [email protected].
- Public 2023-12-16 11:35.
- Последнее изменение 2025-01-23 12:44.
Подсчет дробей - один из самых полезных математических навыков. Прежде чем выполнять дробные вычисления, узнайте, как определять части и типы дробей. После этого их можно складывать или вычитать. Для более сложных вычислений узнайте, как умножать и делить дроби. Обычно вам также нужно упростить или сократить дроби.
Шаг
Метод 1 из 4: распознавание дробей

Шаг 1. Найдите дробь
Дроби записываются одним числом над разделительной линией и другим числом под линией.
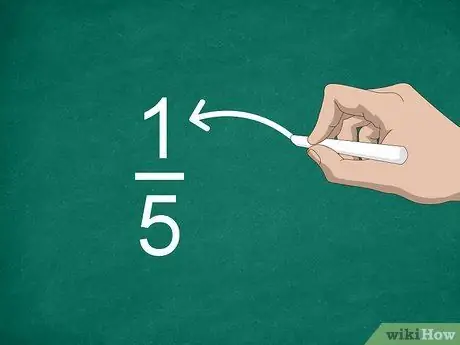
Шаг 2. Определите числитель
Число над линией называется числителем и показывает, сколько частей в дроби.
Например, в дроби 1/5 числитель является «1»
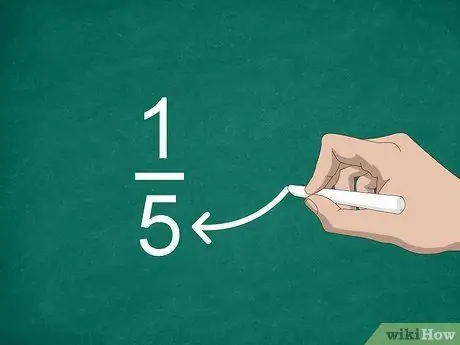
Шаг 3. Найдите знаменатель
Число, помещенное под чертой, называется знаменателем. Это значение указывает количество частей, которые «составляют» целое число.
Например, в дроби 1/5 знаменателем является «5», поэтому дробь состоит из пяти частей

Шаг 4. Определите, являются ли дроби разумными или неправильными
Если числитель меньше знаменателя, дробь является натуральной дробью. В неправильных дробях числитель больше знаменателя.
- Например, 3/4 - это разумная дробь, а 5/3 - неправильная дробь.
- Если у вас есть целое число, которое включает дробь, это число называется смешанным числом. Например, 1 1/2 - смешанное число.
Метод 2 из 4: сложение или вычитание дробей

Шаг 1. Найдите дроби с одинаковым знаменателем
Если вам нужно сложить или вычесть дроби, каждая дробь должна иметь один и тот же знаменатель, прежде чем выполнять расчет. Обратите внимание на знаменатель каждой дроби, чтобы убедиться, что все они равны (похожи).
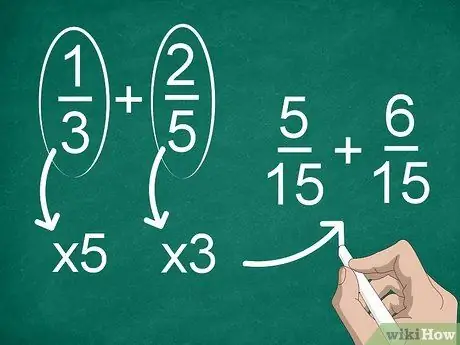
Шаг 2. Найдите общий знаменатель, если у каждой дроби другой знаменатель
Если знаменатели не совпадают, вам нужно будет изменить дроби, чтобы иметь тот же знаменатель. Чтобы найти общий знаменатель, умножьте каждую дробь на знаменатель другой.
Например, чтобы найти общий знаменатель в 1/3 + 2/5, умножьте «1» и «3» на «5», затем умножьте «2» и «5» на «3». Теперь у вас есть сложение 5/15 + 6/15. После этого можно рассчитывать дроби
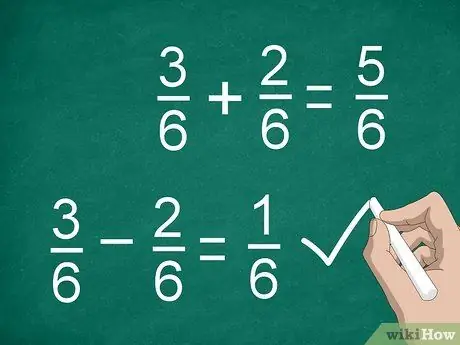
Шаг 3. Сложите или вычтите числители, чтобы вычислить дроби
После того, как вы нашли общий знаменатель и умножили числители (при необходимости), вы готовы складывать или вычитать. Сложите или вычтите числители и поместите результат над разделительной линией. Напишите общий знаменатель под чертой.
- Например, 3/6 - 2/6 = 1/6.
- Не складывайте и не вычитайте знаменатели.
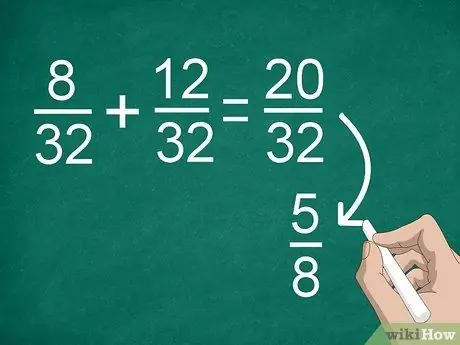
Шаг 4. При необходимости упростите результаты
Если раньше вам нужно было найти общий знаменатель, вы могли бы получить большую дробь, которую можно было бы упростить. Например, если вы добавите 8/32 +12/32, в результате вы получите «20/32». Эту дробь можно упростить до «5/8».
Метод 3 из 4: умножение и упрощение дробей
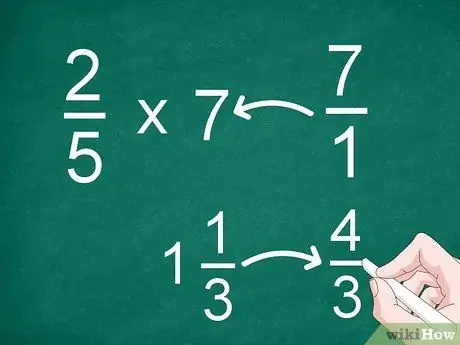
Шаг 1. Преобразуйте смешанные дроби или целые числа в неправильные дроби
Чтобы упростить умножение, вам нужно преобразовать каждое число в разумную или неправильную дробь. Если у вас есть целые или смешанные числа, которые нужно умножить, сначала преобразуйте их в обычную дробь (натуральную или неправильную).
- Например, чтобы умножить 2/5 на 7, преобразуйте 7 в дробь. После этого вы можете умножить 2/5 на 7/1.
- Если у вас смешанное число, например 1 1/3, преобразуйте его в неправильную дробь («4/3») перед умножением.
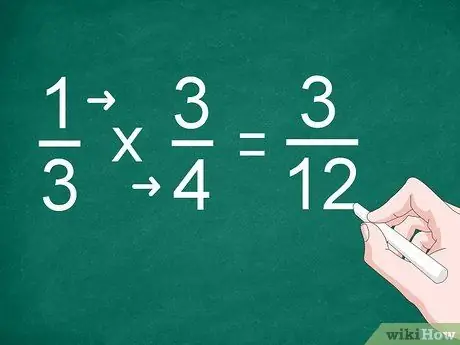
Шаг 2. Умножьте каждый числитель и знаменатель
Вместо того, чтобы делать сложение, умножьте числитель и запишите результат над разделительной линией. Также нужно умножить знаменатели и записать результат под чертой.
Например, чтобы умножить 1/3 на 3/4, умножьте «1» на «3», чтобы получить числитель. Умножьте «3» на «4», чтобы получить знаменатель. Ответ на умножение - «3/12»

Шаг 3. Упростите результаты
Обычно вам нужно будет привести результат к более простому виду, особенно если изначально у вас неестественные дроби. Найдите наибольший общий множитель и используйте этот множитель, чтобы упростить числитель и знаменатель.
Например, для дроби 3/12 наибольший общий делитель между «3» и «12» равен «3». Разделите каждый элемент дроби на «3», пока не получите дробь «1/4»
Метод 4 из 4: разделить дроби
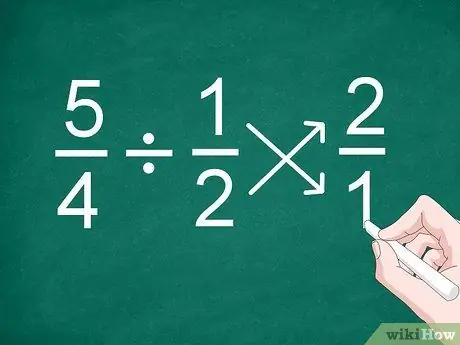
Шаг 1. Поменяйте местами вторую дробь
Самый простой способ разделить дроби, даже дроби с разными знаменателями, - это перевернуть положение второй дроби перед вычислением результата.
Например, для задачи 5/4 1/2 измените положение дроби «1/2» на «2/1»
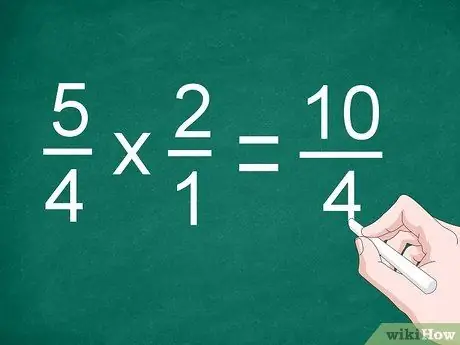
Шаг 2. Умножьте числитель и знаменатель
Умножайте дроби напрямую, чтобы умножить числители. Напишите результат над разделительной линией, затем умножьте знаменатель. Запишите произведение знаменателей под чертой.
В предыдущем примере умножьте 5/4 на 2/1, чтобы получить «10/4»
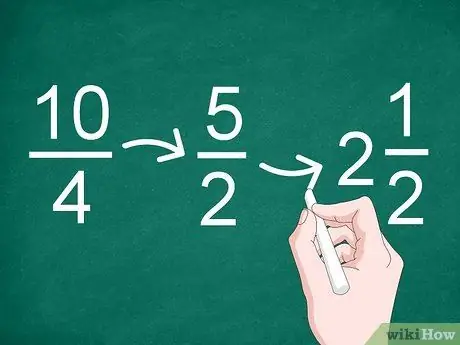
Шаг 3. При необходимости упростите результаты
Если результат деления является неправильной дробью или может быть уменьшен, упростите дробь. Используйте наибольший общий множитель, чтобы уменьшить дробь.
- Например, наибольший общий множитель дроби 10/4 равен «2», поэтому результатом упрощения станет «5/2» (10, разделенное на 2, и 4, разделенное на 2).
- Поскольку результатом упрощения является неправильная дробь, вы можете преобразовать ее в целое и дробное (смешанное число). Следовательно, 5/2 можно изменить на «2».
подсказки
- Если вы работаете со сложными дробями, вам необходимо предпринять некоторые дополнительные шаги, чтобы упростить дробь. Однако само это упрощение является обязательной частью процесса расчета.
- Всегда записывайте дроби аккуратно, чтобы снизить риск просчетов.






