- Автор Jason Gerald [email protected].
- Public 2024-01-16 19:54.
- Последнее изменение 2025-01-23 12:44.
При изучении оптических инструментов «увеличение» линзовидного объекта - это отношение высоты изображения, которое вы видите, к фактической высоте объекта. Например, линза, которая может придать объекту очень большой вид, имеет «высокий» коэффициент увеличения, а линза, которая заставляет объект выглядеть маленьким, имеет «низкий» коэффициент увеличения. Формула увеличения объекта обычно рассчитывается по формуле M = (hя/часо) = - (dя/ до), где M = увеличение, чя = высота изображения, hо = высота объекта, а dя и Dо = расстояние изображения и объекта.
Шаг
Метод 1 из 2: Расчет увеличения одной линзы
Примечания: A собирающая линза в центре шире, чем по краям (как у увеличительного стекла). а расходящаяся линза по краям шире, чем в центре (как чаша). Расчет увеличения на обоих объективах одинаков, с одно важное исключение. Щелкните здесь, чтобы перейти непосредственно к исключениям для расходящихся линз.
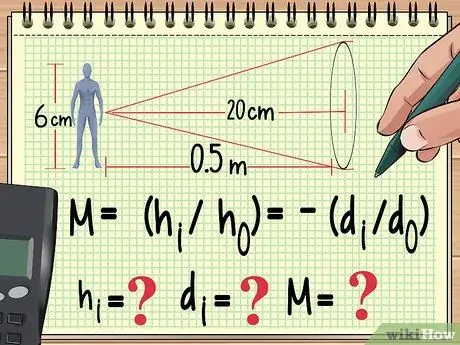
Шаг 1. Начните с вашего уравнения и переменных, которые вы уже знаете
Как и в случае с любой другой физической проблемой, способ решения проблемы увеличения состоит в том, чтобы записать уравнение, которое вы будете использовать для его вычисления. Отсюда вы можете работать в обратном направлении, чтобы найти значение переменной, которую вы не нашли в уравнении, которое вы используете.
-
Например, предположим, что кукла высотой 6 см расположена на расстоянии одного метра от собирающая линза с фокусным расстоянием 20 см. Если мы хотим вычислить увеличение, высоту изображения и расстояние до изображения, мы можем начать писать наше уравнение следующим образом:
-
- M = (hя/часо) = - (dя/ до)
-
- Теперь мы знаем чо (высота куклы) и dо (кукольное расстояние от линзы). Нам также известно фокусное расстояние объектива, которого нет в этом уравнении. Мы посчитаем чася, dя, И м.

Шаг 2. Используя уравнение линзы, получаем dя.
Если вы знаете расстояние от объекта, который вы увеличиваете, и фокусное расстояние объектива, вычислить расстояние до сформированного изображения очень легко с помощью уравнения объектива. Уравнение линзы: 1 / f = 1 / до + 1 / дя, где f = фокусное расстояние объектива.
-
В этом примере задачи мы можем использовать уравнение линзы для вычисления dя. Введите значения f и dя затем решите уравнение:
-
- 1 / f = 1 / до + 1 / дя
- 1/20 = 1/50 + 1 / дя
- 5/100 - 2/100 = 1 / денья
- 3/100 = 1 / дя
- 100/3 = dя = 33,3 см
-
- Фокусное расстояние линзы - это расстояние от центра линзы до точки, где свет проходит в фокусной точке. Если вы когда-либо фокусировали свет с помощью увеличительного стекла на горящих муравьях, вы это видели. В вопросах урока обычно указывается величина этой горячей точки. В реальной жизни эти характеристики обычно пишутся на этикетке, расположенной на объективе.

Шаг 3. Расчет hя.
После вычисления dо и Dя, вы можете рассчитать высоту увеличиваемого объекта и увеличение объектива. Обратите внимание на два знака равенства в уравнении увеличения линзы (M = (hя/часо) = - (dя/ до)) - это означает, что все части этого уравнения равны между собой, поэтому мы можем вычислить M и hя в любом порядке.
-
Для этого примера задачи мы можем вычислить hя нравится:
-
- (чася/часо) = - (dя/ до)
- (чася/6) = -(33, 3/50)
- чася = - (33, 3/50) х 6
- чася = - 3, 996 см
-
- Обратите внимание, что высота объекта здесь отрицательная, что указывает на то, что изображение, которое мы увидим позже, будет перевернуто (сверху вниз).

Шаг 4. Расчет M
Вы можете вычислить последнюю переменную с помощью уравнения - (dя/ до) или (hя/часо).
-
В следующем примере вычисление M выполняется следующим образом:
-
- M = (hя/часо)
-
М = (-3, 996/6) = - 0, 666
-
-
Результат будет таким же при вычислении с использованием значения d:
-
- M = - (dя/ до)
- М = - (33, 3/50) = - 0, 666
-
- Обратите внимание, что у зума нет метки единицы измерения.
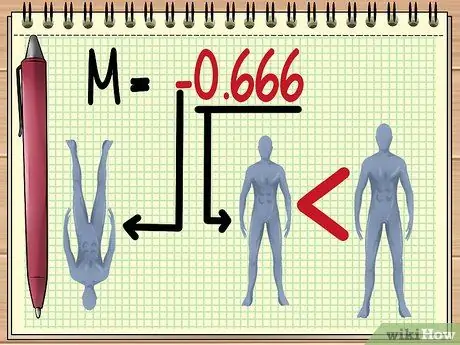
Шаг 5. Понимание значения M
Как только вы получите значение M, вы сможете оценить несколько вещей об изображении, которое увидите через линзу, а именно:
-
Размер.
Чем больше «абсолютное значение» M, тем больше будет объект, рассматриваемый в объектив. Значение M от 0 до 1 указывает, что объект будет выглядеть меньше.
-
Ориентация на объект.
Отрицательное значение указывает, что сформированное изображение будет перевернуто.
- В приведенном здесь примере значение M, равное -0,666, означает, что в соответствии со значением существующей переменной тень куклы будет видна. в перевернутом виде и на две трети меньше действительного размера.
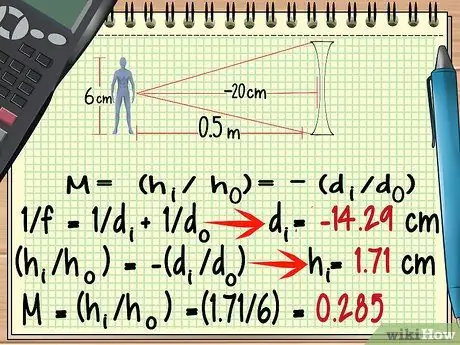
Шаг 6. Для расходящейся линзы используйте отрицательную точку фокусировки
Хотя форма расходящейся линзы сильно отличается от формы собирающей линзы, вы можете рассчитать ее увеличение, используя ту же формулу, что и выше. Следует иметь в виду исключения: Фокус рассеивающей линзы отрицательный.
В приведенном выше примере задачи это повлияет на ответ, который вы получите при вычислении d.я, поэтому обязательно обратите на это внимание.
-
Давайте переработаем приведенный выше пример проблемы, только теперь мы используем расходящуюся линзу с фокусным расстоянием. - 20 см.
Остальные переменные сохраняют то же значение.
-
Прежде всего, вычислим dя используя уравнение линзы:
-
- 1 / f = 1 / до + 1 / дя
- 1 / -20 = 1/50 + 1 / денья
- -5/100 - 2/100 = 1 / дя
- -7/100 = 1 / дя
- -100/7 = dя = - 14, 29 см
-
-
Теперь посчитаем hя и M со значением dя новый.
-
- (чася/часо) = - (dя/ до)
- (чася/6) = -(-14, 29/50)
- чася = - (- 14, 29/50) х 6
- чася = 1, 71 см
- M = (hя/часо)
- М = (1, 71/6) = 0, 285
-
Метод 2 из 2: Расчет увеличения нескольких линз
Простой метод двух линз
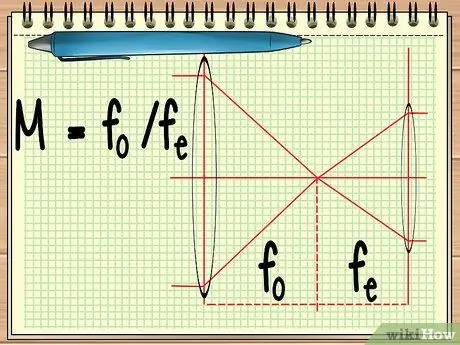
Шаг 1. Рассчитайте фокус двух линз
Когда вы используете инструмент, состоящий из двух линз, расположенных рядом друг с другом (например, телескоп или бинокль), все, что вам нужно выяснить, - это точка фокусировки двух линз, чтобы рассчитать общее увеличение двух линз. это можно вычислить с помощью простого уравнения M = fо/ fе.
В уравнении fо - фокус линзы объектива, а fе фокус окуляра. Линза объектива - это большая линза, которая находится близко к объекту, а окулярная линза - это линза, которая расположена близко к глазу наблюдателя.

Шаг 2. Подставьте уже имеющуюся информацию в уравнение M = fо/ fе.
Когда у вас есть точки фокусировки обеих линз, их очень легко вычислить - вычислить соотношение, разделив фокусное расстояние линзы объектива на фокусное расстояние окуляра. Ответ, который вы получите, - это полное увеличение инструмента.
-
Например, предположим, что в простом телескопе написано, что фокус линзы объектива 10 см, а точка фокусировки окуляра 5 см, тогда увеличение составляет 10/5 = 2.
Сложный метод
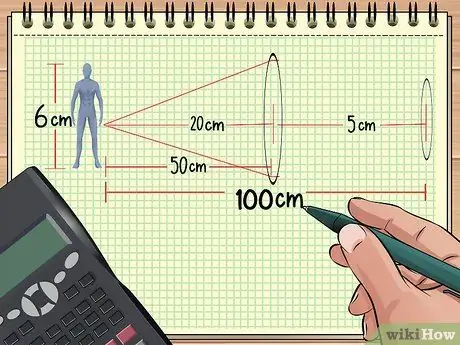
Шаг 1. Рассчитайте расстояние между линзами и объектом
Если у вас есть две линзы, расположенные в ряд перед объектом, общее увеличение можно рассчитать, если вы знаете расстояние от линз до объекта, размер объекта и точку фокусировки двух линз. Остаток также можно рассчитать.
Например, предположим, что мы располагаем объекты и линзы, как в примере задачи 1 выше: кукла находится на расстоянии 50 см от собирающей линзы с фокусным расстоянием 20 см. Теперь поместите вторую линзу с фокусной точкой 5 см на расстоянии 50 см от первой линзы (100 см от куклы). После этого мы рассчитаем общее увеличение, используя полученную информацию
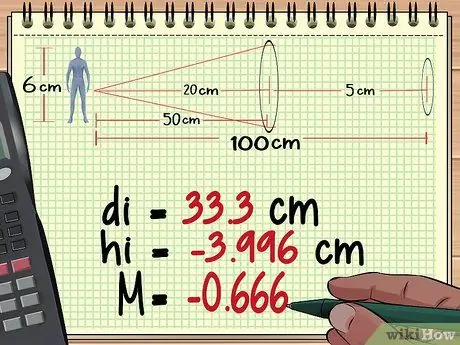
Шаг 2. Рассчитайте расстояние до объекта, высоту и увеличение от линзы 1
Первая часть вычисления увеличения нескольких линз аналогична вычислению увеличения одной линзы. Начните с линзы, ближайшей к объекту, используйте уравнение линзы, чтобы найти расстояние от сформированного изображения, затем используйте уравнение увеличения, чтобы найти высоту и увеличение изображения. Щелкните здесь, чтобы просмотреть больше расчетов увеличения для одного объектива.
-
Из наших вычислений в методе 1 выше мы находим, что первая линза дает изображение с высотой - 3, 996 см, расстояние 33,3 см за объективом, а при увеличении - 0, 666.
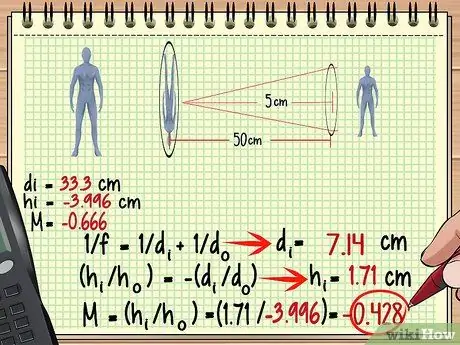
Шаг 3. Используйте изображение с первой линзы как объект со второй линзы
Теперь найти увеличение, высоту и другие параметры для второго объектива очень просто - просто используйте тот же метод, который вы использовали для первого объектива, только на этот раз обрабатывайте изображение как объект. Помните, что расстояние изображения до второй линзы не всегда совпадает с расстоянием от объекта до первой линзы.
-
В приведенном выше примере, поскольку изображение формируется на 33,3 см позади первой линзы, расстояние составляет 50-33,3 = 16,7 см перед второй линзой. Давайте используем это измерение и фокусное расстояние второй линзы, чтобы найти изображение, сформированное второй линзой.
-
- 1 / f = 1 / до + 1 / дя
- 1/5 = 1/16, 7 + 1 / дя
- 0, 2 - 0, 0599 = 1 / дя
- 0, 14 = 1 / дя
- dя = 7, 14 см
-
-
Теперь мы можем вычислить hя и M для второй линзы:
-
- (чася/часо) = - (dя/ до)
- (чася/-3, 996) = -(7, 14/16, 7)
- чася = - (0, 427) х -3, 996
- чася = 1, 71 см
- M = (hя/часо)
- М = (1, 71 / -3, 996) = - 0, 428
-
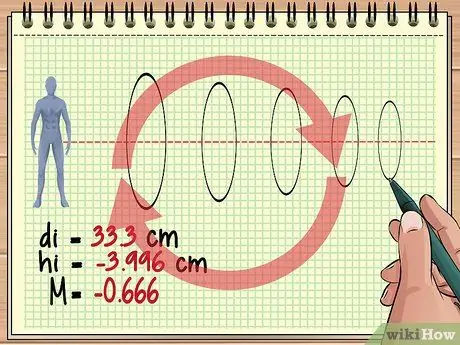
Шаг 4. Продолжите такие же вычисления для дополнительных линз
Этот базовый подход одинаков, если перед объектом выстроены три, четыре или сотни линз. Для каждой линзы рассмотрите изображение предыдущей линзы как объект и используйте уравнение линзы и уравнение увеличения, чтобы найти нужный ответ.
Имейте в виду, что каждая последующая линза может непрерывно инвертировать сформированное изображение. Например, значение увеличения, которое мы получили ранее (-0, 428), указывает на то, что изображение, которое мы собираемся увидеть, составляет примерно 4/10 фактического размера объекта, но перпендикулярно, потому что изображение с предыдущего объектива инвертировано
подсказки
- Бинокли обычно предоставляют объяснение характеристик увеличения в виде числа, умноженного на несколько. Например, бинокль можно указать как 8x25 или 8x40. Когда написано так, первое число - это увеличение бинокля. Это не имеет значения, даже если в приведенном примере два числа различаются по величине, оба бинокля имеют 8-кратное увеличение. Второе число указывает, насколько четкое изображение будет формироваться в бинокль.
- Помните, что для однообъективной лупы увеличение будет отрицательным, если расстояние до объекта больше фокусного расстояния объектива. Это не значит, что сформированное изображение будет меньше. В этом случае увеличение все еще происходит, но сформированное изображение будет видно наблюдателю в перевернутом виде (сверху вниз).






