- Автор Jason Gerald [email protected].
- Public 2023-12-16 11:35.
- Последнее изменение 2025-01-23 12:44.
Сложение дробей - очень полезное знание. Этот навык очень легко освоить и использовать при работе над математическими задачами от начальной до средней школы. В этой статье объясняется, как складывать дроби, чтобы вы могли сделать это всего за несколько минут.
Шаг
Метод 1 из 2: сложение дробей с одинаковым знаменателем

Шаг 1. Проверьте знаменатель (число под частным) каждой дроби
Если числа совпадают, значит, вы складываете дроби с одинаковым знаменателем. Если знаменатели разные, прочтите второй способ.
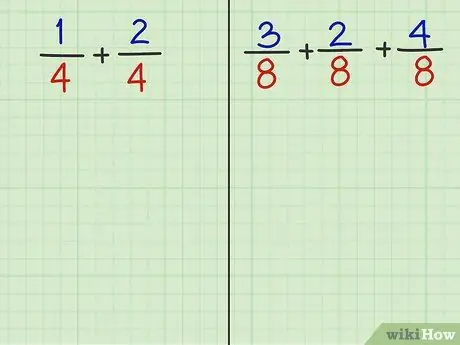
Шаг 2. Ответьте на следующие 2 вопроса
Прочитав последний шаг этого метода, вы сможете сложить доли следующих двух вопросов.
- Проблема 1: 1/4 + 2/4
- Проблема 2: 3/8 + 2/8 + 4/8
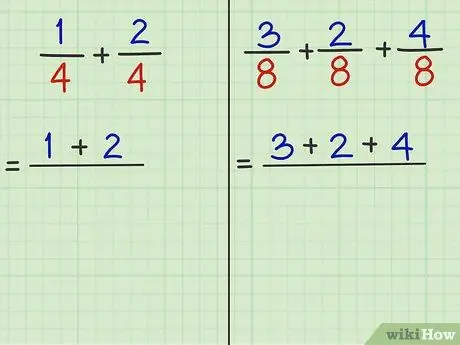
Шаг 3. Соберите числители (числа над разделителем) и сложите их
В числителе указывается число над частным. Независимо от того, сколько дробей вы хотите сложить, вы можете сразу же добавить числители, если знаменатели совпадают.
- Проблема 1: 1/4 + 2/4 - добавляемая дробь. «1» и «2» - числители. Итак, 1 + 2 = 3.
- Проблема 2: 3/8 + 2/8 + 4/8 - это дробная часть, которую нужно добавить. «3», «2» и «4» - числители. Итак, 3 + 2 + 4 = 9.

Шаг 4. Определите новую дробь из суммы
Запишите числитель, полученный на шаге 2. Это число новый числитель. Напишите знаменатель, который представляет собой то же число под биссектрисой каждой дроби. Если знаменатели совпадают, производить вычисления не нужно. Это число новый знаменатель и всегда равняется старому знаменателю, когда вы складываете дроби с тем же знаменателем.
- Проблема 1: 3 - новый числитель, а 4 - новый знаменатель. Таким образом, ответ на вопрос 1 - 3/4. 1/4 + 2/4 = 3/4.
- Проблема 2: 9 - новый числитель, а 8 - новый знаменатель. Таким образом, ответ на вопрос 2 - 9/8. 3/8 + 2/8 + 4/8 = 9/8.
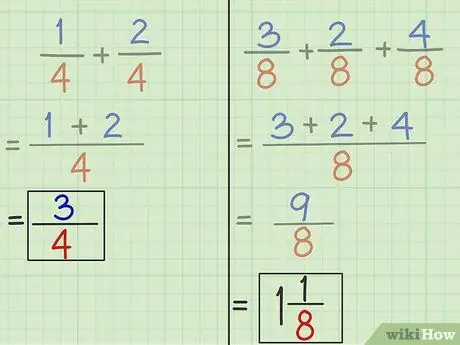
Шаг 5. При необходимости упростите дроби
Не забудьте упростить новую дробь, чтобы упростить запись.
-
Если числитель больше вместо знаменателя, такого как результат сложения задачи 2, это означает, что после упрощения дроби мы получаем целый месяц. Разделите числитель на знаменатель или 9 разделите на 8. В результате останется целое число 1. Запишите целые числа перед дробью, а остаток становится числителем новой дроби с тем же знаменателем.
9/8 = 1 1/8.
Метод 2 из 2: сложение дробей с разными знаменателями

Шаг 1. Проверьте знаменатель (число под частным) каждой дроби
Если знаменатели разные, вы складывать дроби с разными знаменателями. Прочтите следующие шаги, потому что вы должны уравнять знаменатели перед сложением дробей.
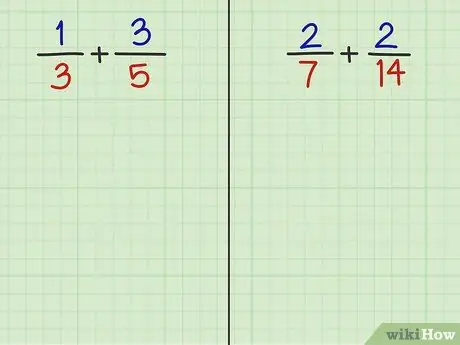
Шаг 2. Решите следующие 2 вопроса
Прочитав последний шаг этого метода, вы сможете сложить доли следующих двух вопросов.
- Проблема 3: 1/3 + 3/5
- Вопрос 4: 2/7 + 2/14

Шаг 3. Совместите знаменатели
Для этого умножьте знаменатели двух указанных выше дробей. Простой способ уравнять знаменатели - это умножить знаменатели двух дробей. Если один из знаменателей кратен другому, найдите наименьшее общее кратное для двух знаменателей.
-
Проблема 3:
3 x 5 = 15. Итак, новый знаменатель обеих дробей равен 15.
-
Проблема 4:
14 делится на 7. Следовательно, нам нужно только умножить 7 на 2, чтобы получить 14. Таким образом, новый знаменатель обеих дробей равен 14.

Шаг 4. Умножьте числитель и знаменатель первой дроби на знаменатель второй дроби
Этот шаг не изменяет значение дроби, но дробь выглядит так, чтобы соответствовать знаменателю. Дробное значение остается прежним.
-
Проблема 3:
1/3 х 5/5 = 5/15.
-
Проблема 4:
Для этой задачи нам просто нужно умножить первую дробь на 2/2, чтобы знаменатели стали равными.
2/7 х 2/2 = 4/14

Шаг 5. Умножьте числитель и знаменатель второй дроби на знаменатель первой дроби
Как и в предыдущих шагах, мы не меняем значение дроби, но дробь выглядит измененной, чтобы уравнять знаменатель. Дробное значение остается прежним.
-
Проблема 3:
3/5 х 3/3 = 9/15.
-
Проблема 4:
Нам не нужно умножать вторую дробь, потому что знаменатели совпадают.

Шаг 6. Запишите две новые дроби по порядку
На данный момент мы не сложили две дроби вместе, хотя можем. На предыдущем шаге мы умножили каждую дробь на 1. Теперь мы хотим убедиться, что дроби, которые мы хотим сложить, имеют одинаковый знаменатель.
-
Проблема 3:
вместо 1/3 + 3/5 дробь становится 5/15 + 9/15
-
Проблема 4:
Вместо 2/7 + 2/14 дробь становится 4/14 + 2/14.

Шаг 7. Сложите числители двух дробей
В числителе указывается число над частным.
-
Проблема 3:
5 + 9 = 14. 14 - новый числитель.
-
Проблема 4:
4 + 2 = 6. 6 - новый числитель.

Шаг 8. Запишите общий знаменатель (на шаге 2) под новым числителем или используйте знаменатель дроби, умноженной на 1, чтобы выровнять знаменатель
-
Проблема 3:
15 - новый знаменатель.
-
Проблема 4:
14 - новый знаменатель.

Шаг 9. Напишите новый числитель и новый знаменатель
-
Проблема 3:
14/15 - это ответ 1/3 + 3/5 =?
-
Проблема 4:
6/14 - это ответ 2/7 + 2/14 =?

Шаг 10. Упростите и сократите дроби
Чтобы упростить дроби, разделите числитель и знаменатель на наибольший общий делитель двух чисел.
-
Проблема 3:
14/15 не может быть упрощено.
-
Проблема 4:
6/14 можно уменьшить до 3/7 после деления числителя и знаменателя на 2 как наибольший общий делитель 6 и 14.
подсказки
- Перед сложением дробей убедитесь, что знаменатели совпадают.
- Не складывайте знаменатели. Если знаменатели совпадают, используйте число в качестве знаменателя после сложения дробей.
- Если вы хотите сложить дроби с числами, состоящими из целых чисел и дробей, преобразуйте эти числа в дроби и сложите их в соответствии с приведенными выше инструкциями.






