С помощью коэффициента ранговой корреляции Спирмена мы можем определить, имеют ли две переменные монотонную функциональную связь (то есть, когда одно число увеличивается, другое число также увеличивается, или наоборот). Чтобы вычислить коэффициент ранговой корреляции Спирмена, вам необходимо ранжировать и сравнивать наборы данных, чтобы найти d2, а затем введите данные в стандартную или упрощенную формулу коэффициента ранговой корреляции Спирмена. Вы также можете рассчитать эти коэффициенты с помощью формул Excel или команды R.
Шаг
Метод 1 из 3: ручной способ
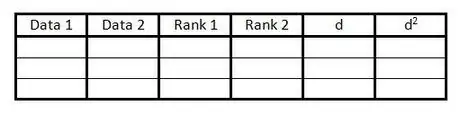
Шаг 1. Создайте таблицу
Таблица используется для включения всей информации, необходимой для расчета коэффициента корреляции рангов Спирмена. Вам нужна такая таблица:
- Создайте 6 столбцов с заголовками, как в примере.
- Подготовьте столько пустых строк, сколько пар данных.
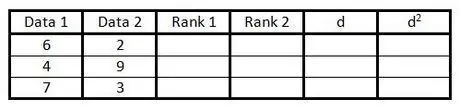
Шаг 2. Заполните первые два столбца парами данных
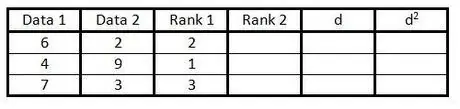
Шаг 3. Введите ранжирование первого столбца групп данных в третий столбец от 1 до n (количество данных)
Дайте оценку 1 для наименьшего значения, оценку 2 для следующего наименьшего значения и так далее.
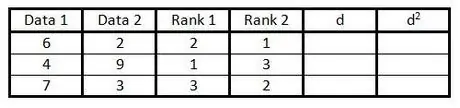
Шаг 4. В четвертом столбце сделайте то же, что и на шаге 3, но для ранжирования данных во втором столбце
-
Среднее_742 Если есть два (или более) данных, которые имеют одинаковое значение, вычислите средний рейтинг данных, а затем введите его в таблицу на основе этого среднего значения.
В примере справа есть два значения 5 для оценок 2 и 3. Поскольку есть две 5, найдите среднее значение оценок. Среднее значение 2 и 3 составляет 2,5, поэтому введите значение рейтинга 2,5 для обоих значений 5.
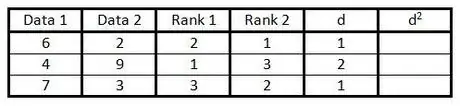
Шаг 5. В столбце «d» вычислите разницу между двумя числами в столбце ранга
То есть, если один столбец имеет рейтинг 1, а другой столбец - 3, разница составляет 2. (Знак не имеет значения, потому что следующим шагом будет возведение значения в квадрат).
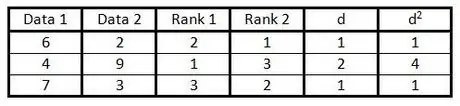
Шаг 6. Возвести в квадрат каждое число в столбце «d» и записать результат в столбец «d».2".
Шаг 7. Сложите все данные в столбце "d".2".
Результат d2.
Шаг 8. Выберите одну из следующих формул:
-
Если ни один из рейтингов не является таким же, как на предыдущем шаге, введите это значение в упрощенную формулу коэффициента корреляции рангов Спирмена.
Step8_271 и замените «n» на количество пар данных, чтобы получить результат.
Step9_402 -
Если на предыдущем шаге есть аналогичный ранг, используйте стандартную формулу коэффициента корреляции рангов Спирмена:
Spearman
Шаг 9. Интерпретируйте результаты
Значение может варьироваться от -1 до 1.
- Если значение близко к -1, корреляция отрицательная.
- Если значение близко к 0, линейной корреляции нет.
- Если значение близко к 1, корреляция положительная.
Метод 2 из 3: Использование Excel
Шаг 1. Создайте новый столбец для данных вместе с его рейтингом
Например, если ваши данные находятся в столбце A2: A11, используйте формулу «= RANK (A2, A $ 2: A $ 11)» и копируйте ее, пока она не покроет все столбцы и строки.
Шаг 2. Измените рейтинг, как описано в шагах 3 и 4 метода 1
Шаг 3. В новой ячейке вычислите корреляцию между двумя ранговыми столбцами по формуле «= КОРРЕЛЬ (C2: C11, D2: D11)»
В этом примере C и D относятся к столбцу, в котором находится рейтинг. Новая ячейка будет заполнена корреляцией рангов Спирмена.
Метод 3 из 3: Использование R
Шаг 1. Сначала установите программу R, если у вас ее еще нет
(См.
Шаг 2. Сохраните данные в формате CSV, поместите данные, для которых вы хотите найти корреляцию, в первые два столбца
Мы можем сделать это с помощью меню «Сохранить как».
Шаг 3. Откройте редактор R
Если вы работаете с терминала, просто запустите R. Если вы работаете с рабочего стола, щелкните значок R.
Шаг 4. Введите следующую команду:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") и нажмите Enter.
- cast (rank (d [, 1]), rank (d [, 2]))
подсказки
Данные должны состоять как минимум из 5 пар, чтобы можно было увидеть тенденцию (количество данных составляет 3 пары в примере только для упрощения вычислений)
Предупреждение
- Коэффициент ранговой корреляции Спирмена определяет только силу корреляции, когда данные постоянно растут или падают. Если в данных есть другая тенденция, ранговая корреляция Спирмена нет обеспечит точное представление.
- Эта формула основана на предположении, что нет равных рейтингов. Когда есть такой же ранг, как в примере, мы должны использовать это определение: коэффициент корреляции момента умножения по рангу.
