- Автор Jason Gerald [email protected].
- Public 2024-01-19 22:14.
- Последнее изменение 2025-01-23 12:44.
Математика - это сложно. Легко забыть даже основные концепции, если вы попытаетесь запомнить множество различных принципов и методов. Вот два новых способа упростить дроби.
Шаг
Метод 1 из 4: Использование наибольшего общего множителя

Шаг 1. Запишите множители числителя и знаменателя
Факторы - это числа, которые можно умножить, чтобы получить другое число. Например, 3 и 4 являются делителями 12, потому что вы можете умножить их вместе, чтобы получить 12. Чтобы записать множители числа, вам просто нужно записать все числа, которые можно умножить, чтобы получить это число, и которые являются делимыми. по факторам.
-
Запишите множители числа от наименьшего к наибольшему, не забывая включить множитель 1. Например, вот как вы записываете числитель и знаменатель дроби 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Шаг 2. Найдите наибольший общий делитель числителя и знаменателя
GCF - это наибольшее число, которое может равномерно разделить два или более числа. После того, как вы записали все факторы числа, все, что вам нужно сделать, это найти наибольшее число, которое одинаково в обоих списках факторов.
-
24: 1, 2, 3, 4, 6,
Шаг 8., 12, 24.
-
32: 1, 2, 4,
Шаг 8., 16, 32.
-
GCF 24 и 32 равно 8, потому что 8 - это наибольшее число, которое может равномерно разделить 24 и 32.

Шаг 3. Разделите числитель и дробь на GCF
Теперь, когда у вас есть GCF, все, что вам нужно сделать, это разделить числитель и знаменатель на это число, чтобы упростить дробь до ее простейшего вида. Вот как это сделать:
- 24/8 = 3
- 32/8 = 4
- Простая дробь - 3/4.

Шаг 4. Проверьте свою работу
Если вы хотите убедиться, что вы упростили дробь правильно, вам просто нужно умножить новый числитель и знаменатель на их GCF, чтобы вернуть исходную дробь. Вот как это сделать:
- 3 * 8 = 24
- 4 * 8 = 32
-
Вы вернулись в исходный вид, то есть 24/32.
Вы также можете проверить дробь, чтобы убедиться, что ее нельзя упростить. Поскольку 3 является простым числом, его можно разделить только на 1 и само себя, а четыре не делится на 3, поэтому дробь не может быть упрощена
Метод 2 из 4: продолжайте делить на маленькие числа

Шаг 1. Выберите небольшое число
Используя этот метод, вам нужно для начала выбрать небольшое число, например 2, 3, 4, 5 или 7. Посмотрите на дроби, чтобы убедиться, что каждая часть делится на выбранное вами число. Например, если у вас дробь 24/108, не выбирайте 5, потому что она не делится на 5. Однако, если у вас дробь 25/60, правильным числом будет 5.
Для дроби 24/32 2 - хорошее число. Поскольку оба числа четные, они делятся на 2

Шаг 2. Разделите числитель и знаменатель дроби на число
Новая дробь будет состоять из нового числителя и знаменателя, которые вы получите после деления верхней и нижней части дроби 24/32 на 2. Вот как это сделать:
- 24/2 = 12
- 32/2 = 16
- Ваша новая дробь - 12/16.
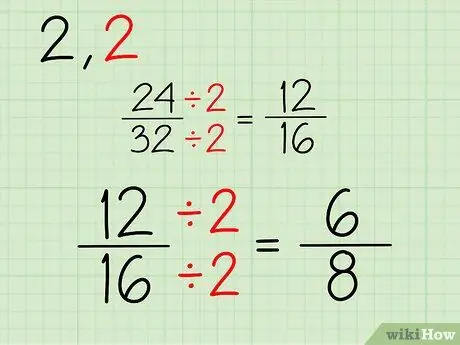
Шаг 3. Повторите
Продолжайте этот процесс. Поскольку оба числа являются четными числами, вы можете продолжать деление на 2. Если один или оба числителя и знаменателя являются нечетными числами, вы можете попробовать разделить их на другое число. Вот процесс упрощения дроби 12/16:
- 12/2 = 6
- 16/2 = 8
- Ваша новая дробь - 6/8.

Шаг 4. Продолжайте делить число, пока оно не перестанет делиться
Новые числитель и знаменатель также являются четными числами, поэтому вы можете продолжать деление на 2. Вот как это сделать:
- 6/2 = 3
- 8/2 = 4
- Ваша новая дробь - 3/4.

Шаг 5. Убедитесь, что дробь больше не может быть упрощена
В дроби 3/4 3 - простое число, поэтому множители равны только 1 и самому себе, а 4 не делится на 3, поэтому дробь не может быть упрощена дальше. Если числитель или знаменатель дроби больше не может быть разделен на выбранное вами число, вы все равно можете разделить его на другое число.
Например, если у вас есть дробь 10/40, и вы разделите числитель и знаменатель на 5, результат будет 2/8. Вы не можете продолжать делить числитель и дробь на 5, но вы можете разделить их на 2, так что конечный результат будет 1/4

Шаг 6. Проверьте свою работу
Умножьте 3/4 на 2/2 еще раз три раза, чтобы убедиться, что вы получили начальную дробь, которая равна 24/32. Вот как это сделать:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Обратите внимание, что вы делите 24/32 на 2 * 2 * 2, что аналогично делению на 8, наибольший GCF 24 и 32.
Метод 3 из 4: написание факторов

Шаг 1. Запишите свою дробь
В правой части листа оставьте большое пространство - оно понадобится вам, чтобы записать факторы.

Шаг 2. Запишите множители числителя и знаменателя
Только факторы двух. Самый простой способ - написать факторы друг над другом. Начните с цифры 1 и запишите коэффициенты.
-
Например, если ваша дробь 24/60, начните с 24.
Запишите: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Затем число 60.
Запишите: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Шаг 3. Найдите и разделите на наибольший общий делитель
Этот термин может быть записан в вашей печатной книге как GCF. Какое наибольшее число может разделить числитель и знаменатель? Независимо от числа, разделите оба числа на это число.
В нашем примере наибольшее число, которое является множителем обоих чисел, равно 12. Таким образом, мы делим 24 на 12 и 60 на 12, что дает нам 2/5 - нашу простую дробь
Метод 4 из 4: Использование дерева основных факторов

Шаг 1. Найдите простые множители числителя и знаменателя
Простое число - это число, которое нельзя разделить ни на какое другое число (кроме самого себя и, конечно же, 1). 2, 3, 5, 7 и 11 являются примерами простых чисел.
- Начнем с числителя. Из 24 разделите на 2 и 12. Поскольку 2 уже является простым числом, вам больше не нужно его делить! Затем разбейте 12 на 2 числа: 2 и 6. 2 - простые числа - отлично! Теперь разделите 6 на 2 числа: 2 и 3. Теперь у вас есть 2, 2, 2 и 3 в качестве простых чисел.
- Теперь поработаем над знаменателем. Из 60 разделите дерево на 2 и 30. 30 затем разделите на 2 и 15. Затем разделите 15 на 3 и 5, которые являются простыми числами. Теперь у вас есть простые числа 2, 2, 3 и 5.
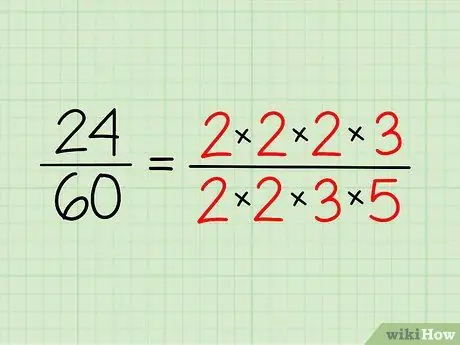
Шаг 2. Запишите факторизацию каждого числа на простые множители
Запишите простые числа, которые у вас есть для каждого числа, и запишите их в форме умножения. Вам не нужно его умножать - это просто способ сделать его более заметным.
- Итак, для 24 у вас есть 2 x 2 x 2 x 3 = 24.
- Для 60 у вас есть 2 x 2 x 3 x 5 = 60

Шаг 3. Устраните те же факторы
Любое число, входящее в оба числа, можно отбросить. В этом примере равными множителями являются пара двоек и одна тройка. До свидания!
- Остальные 2 и 5 - или 2/5! Тот же ответ, что и выше.
- Если числитель и знаменатель дроби - четные числа, не делите просто на два. Продолжайте делать деление до тех пор, пока полученное число не может быть снова разделено.






