- Автор Jason Gerald [email protected].
- Public 2024-01-15 08:22.
- Последнее изменение 2025-01-23 12:44.
Есть разные способы сделать разделение. Вы можете делить десятичные дроби, дроби или даже показатели степени, а также использовать длинное или короткое деление. Если вы хотите узнать о различных способах деления чисел, выполните следующие действия.
Шаг
Метод 1 из 5: Деление длинных серий

Шаг 1. Запишите вопросы
Чтобы выполнить деление в столбик, поместите знаменатель (число, которое будет делиться) за чертой делителя, а числитель (число, которое нужно разделить) внутри черты делителя.
Например: 136 ÷ 3

Шаг 2. Разделите первую цифру числителя на знаменатель (если возможно)
В этом примере 1 не делится на 3, поэтому поставьте 0 над полосой делителя и переходите к следующему шагу. Вычтите 1 на 0 и поместите результат под цифрой 1.

Шаг 3. Разделите остаток первой цифры числителя и второй цифры числителя на знаменатель
Поскольку 1 нельзя разделить на 3, число 1 по-прежнему используется. Вам нужно вычесть 3. Теперь разделите 13 на 3. Поскольку 3 x 4 = 12, поместите 4 над полосой делителя (справа от 0), затем вычтите 13 на 12 и запишите результат под ней.

Шаг 4. Разделите оставшиеся числа на знаменатель
Опустите число 6 справа от 1, чтобы получить 16. Теперь разделите 16 на 3. Поскольку 3 x 5 = 15, запишите число 5 справа от числа 4, вычтите 16 на 15 и запишите результат (16-15 = 1) ниже.

Шаг 5. Напишите остаток рядом с частным
Ваш окончательный ответ - 45 с оставшимся 1, или 45 R1.
Метод 2 из 5: Выполнение коротких делений

Шаг 1. Запишите вопросы
Напишите знаменатель (число, которое нужно разделить) за чертой делителя, а числитель (число, которое нужно разделить) внутри черты делителя. Обратите внимание, что при кратком делении знаменатель не может состоять более чем из одной цифры.
Например, 518 4

Шаг 2. Разделите первую цифру числителя на знаменатель
5 4 = 1 R1. Поместите частное (1) над длинной разделительной полосой. Напишите остаток над первой цифрой числителя. Поместите маленькую 1 на 5, чтобы напомнить вам, что у вас осталась 1, когда вы разделите 5 на 4. Теперь 518 должно выглядеть так: 5118

Шаг 3. Разделите полученное из остатка и второй цифры числителя число на знаменатель
Следующее число - 11, которое получается из остаточной стоимости (1) и второй цифры числителя (1). 11 4 = 2 R 3, потому что 4 x 2 = 8 с остатком 3. Запишите остаточное значение над второй цифрой числителя. Положим 3 вместо 1. Начальный числитель (518) теперь выглядит так: 51138

Шаг 4. Разделите оставшиеся числа на знаменатель
Осталось 38; число 3 происходит от остатка от предыдущего этапа, а 8 - это последняя цифра числителя. Вычислите 38 4 = 9 R2. Поскольку 4 x 9 = 36, напишите «R2» над полосой деления, потому что 38 - 36 = 2.

Шаг 5. Запишите окончательный ответ
Окончательный результат и частное находятся над полосой делителя. Ответ: 518 4 = 129 R2.
Метод 3 из 5: разделить дроби

Шаг 1. Запишите вопросы
Чтобы разделить дробь, просто запишите первую дробь, затем символ деления, а затем вторую дробь.
Например: 3/4 5/8

Шаг 2. Поменяйте местами числитель и знаменатель второй дроби
Вторая дробь теперь обратная.
Пример: 3/4 8/5

Шаг 3. Измените символ деления на символ времени
Чтобы разделить дробь, вы умножаете первую дробь на обратную величину второй.
Пример: 3/4 x 8/5
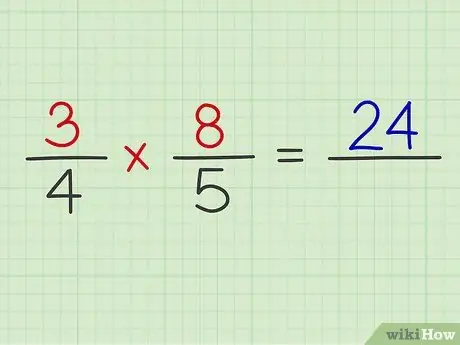
Шаг 4. Умножьте числитель обеих дробей
Просто делайте это как умножение двух обыкновенных дробей.
Пример: 3 х 8 = 24
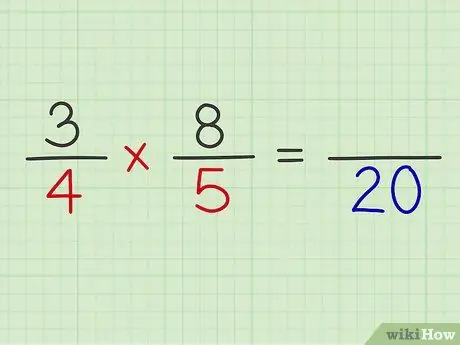
Шаг 5. Умножьте знаменатели обеих дробей
Завершите расчет, умножив две дроби.
Пример: 4 х 5 = 20
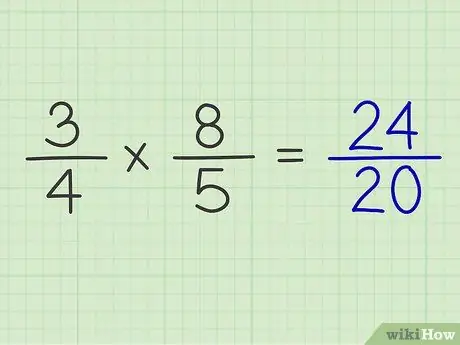
Шаг 6. Положите произведение числителя над произведением знаменателя
Умножив числитель и знаменатель двух дробей, можно получить результат вычисления обеих дробей.
Пример: 3/4 x 8/5 = 24/20

Шаг 7. Упростите дроби
Чтобы найти наибольший общий множитель или наибольшее число, которое делит числитель и знаменатель поровну. В данном случае наибольший общий делитель 24 и 20 равен 4. Чтобы доказать это, запишите все числители и знаменатели и обведите в кружок количество наибольших общих делителей обоих.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- Поскольку 4 является наибольшим общим делителем 24 и 20, просто разделите два числа на 4, чтобы упростить дробь.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

Шаг 8. Перепишите дробь как смешанное число (необязательно)
Уловка, просто разделите числитель на знаменатель и запишите результат в виде целого числа. После этого запишите остаток деления в новом числителе, и знаменатель дроби не изменится. Поскольку деление 6 на 5 дает 1 с остатком 1, запишите целое число 1, затем новый числитель 1, а затем знаменатель 5, чтобы получить смешанное число 1 1/5.
Пример: 6/5 = 1 1/5
Метод 4 из 5: разделить экспоненту

Шаг 1. Убедитесь, что показатели степени / степени имеют одинаковое базовое число
Вы можете делить экспоненты только в том случае, если они имеют одинаковое базовое число. В противном случае вы можете попробовать манипулировать ими, пока не получите такое же базовое число.
Пример: x8 Икс5

Шаг 2. Вычтите показатель степени
Вы можете просто вычесть первый показатель степени на второй. Пока не обращайте внимания на базовые числа.
Пример: 8-5 = 3
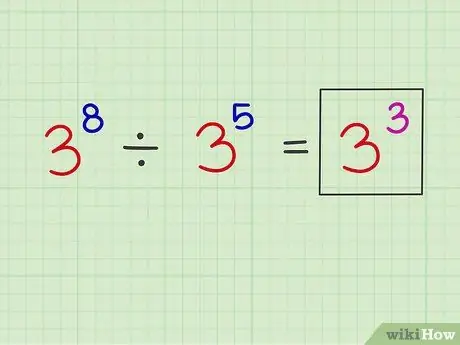
Шаг 3. Поместите новый показатель выше исходного числа
Теперь вы можете написать новую экспоненту над исходным числом.
Пример: x8 Икс5 = х3
Метод 5 из 5: деление десятичных чисел

Шаг 1. Запишите вопросы
Напишите знаменатель (число, которое нужно разделить) за чертой делителя, а числитель (число, которое нужно разделить) внутри черты делителя. В десятичном делении ваша цель - преобразовать десятичное число в целое.
Пример: 65,5.5

Шаг 2. Измените знаменатель на целое число
Просто сдвиньте десятичную запятую на одну цифру вправо, чтобы изменить 0,5 на 5, иначе 5,0.

Шаг 3. Измените числитель, сдвинув десятичную запятую на то же количество цифр, что и знаменатель
Поскольку вы перемещаете десятичную запятую в числителе на одну цифру вправо, чтобы получилось целое число, десятичная точка знаменателя также сдвигается на одну цифру вправо, так что 65,5 изменяется на 655.
Если вы переместите десятичную точку числителя за пределы всех его цифр, это означает, что вам нужно добавлять нули к цифрам при каждом смещении десятичной точки. Например, если десятичная точка 7, 2 сдвинута на три цифры вправо, число изменится на 7200, потому что двухзначный пробел заполнен нулями

Шаг 4. Поместите десятичную точку на полосе длинного деления чуть выше десятичной точки в числителе
Поскольку вы сдвигаете десятичную точку на одну цифру, чтобы получить 0,5 целого числа, рекомендуется разместить десятичную точку над полосой деления именно там, где сдвинута десятичная точка, то есть после последних 5 из 655.

Шаг 5. Решите задачу простым делением в столбик
Чтобы разделить 655 на 5, выполните следующие действия:
- Разделите цифру сотен в числителе (6) на знаменатель (5). Результат - 1 с остатком 1. Напишите число 1 над чертой делителя и напишите 5 под числом 6, которое нужно вычесть.
- Остаток от 1 вычитается из разряда десятков числителя (5), так что теперь вы получаете 15. Разделите 15 на 5, чтобы получить 3. Напишите 3 над полосой делителя справа от 1.
- Отбросьте последние 5 цифр. Разделите 5 на 5, чтобы получить 1. Напишите число 1 над чертой делителя справа от числа 3. Остатка нет, потому что 5 делится на 5.
- Ответ длинного последовательного деления: 655 5 = 131. Этот результат совпадает с ответом на вопросы 65,5 0,5.






